Challenging Geometry Puzzle: Problem 1569. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.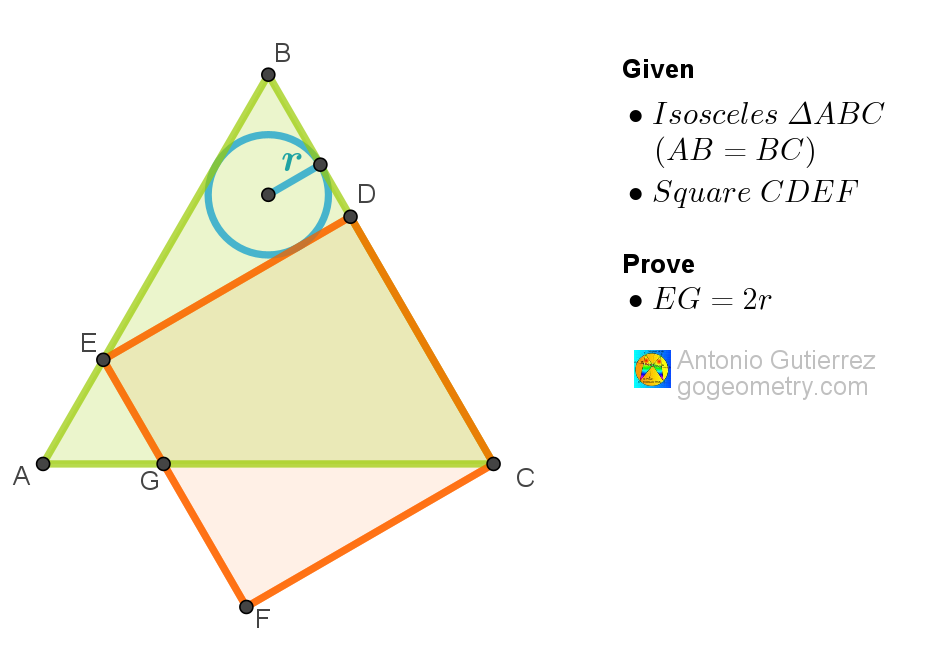
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Trigonometry Solution
ReplyDeleteLet the Incentre of Triangle BED be O and let DE be tangent to the incircle at K & let BD be tangent to the Incircle at L
So KOLD is a Square of side r
Let the Square CDEF be of side u and let AE = EG = v
Let t = tan A
From Triangle EOK,
r/ (u-r) = tan (A-45) = (t-1)/(t+1) from which upon simplification
u = r(2t/(t-1)).............. (1)
From Triangle CFG,
u/(u-v) = t so v/u = (t-1)/t............. (2)
(1) X (2)
v = 2r or EG = 2r
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/LwBnYrJzUHqLL1NQ8
ReplyDeleteConnect CE and we have angle ECD=45
Triangle BED is a right triangle and triangle AEG is isosceles
We have 2r= BD+ED-BE
But BD+ED= BD+DC= BC=BA( triangle ABC is isosceles)
So 2r= BA-BE= AE=EG
Geometry Solution
ReplyDeleteLet the circle (Centre O) be tangent to AD at P, ED at Q and BE at S
Let the square be of side u and let AB = BC = a
Now OPDQ is a square of side r
So EQ = u - r = ES and
Also BP = BC - PC = a - u - r = BS
Hence AE = AB - ES - BS = a - (u - r) - (a - u - r) = 2r
Now EG // BC hence AE = EG = 2r
Sumith Peiris
Moratuwa
Sri Lanka
My surprising solution at my blog, https://stanfulger.blogspot.com/2024/10/gogeometry-pb-1569.html
ReplyDelete