Challenging Geometry Puzzle: Problem 1567. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.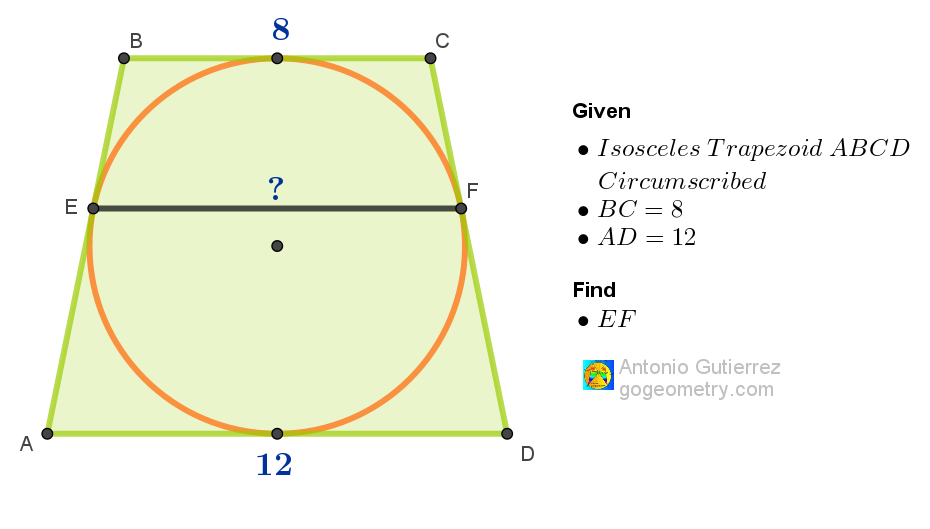
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
https://photos.app.goo.gl/4WgWRasMpNf8eKLj8
ReplyDeleteDefine points M, N, O, K, G, H per attached sketch
Note that NC=CF=4
And OG=¼(8+12)= 5 and KD=1
OF=OM=GK= r
Triangle CHF similar to GKD ( case AA)
So HF/4= ⅕ => HF= ⅘
And EF= BC+ 2.HF= 9.6
Let K,L,M the midpoints BC,AD, EF respectively and O the circumcenter.
ReplyDeleteKL┴EF. Let BG┴AD , CH┴AD (G,H on AD)
GH=BC=8, BG=KL=CH
TrGAB=TrHDC so AG=DH=(AD-GH)/2=2
AB=AE+BE=AL+BK=6+4=10
From Pythagorean Theorem at GAB we have GB^2=AB^2-AG^2
GB=4sqrt(6)
Also is BE/AB=KM/KL (Thales)→ KM=8sqrt(6)/5 hence OM=KL-KM=2sqrt(6)/5
In right triangle MOE we have EM^2=OE^2-OM^2=576/25 → EM=24/5
Therefore EF=2EM=48/5=9.6
Georgios Kousinioris
Gastouni
Hellas