Geometry Problem 1542. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Get the full picture! Click below to uncover the details.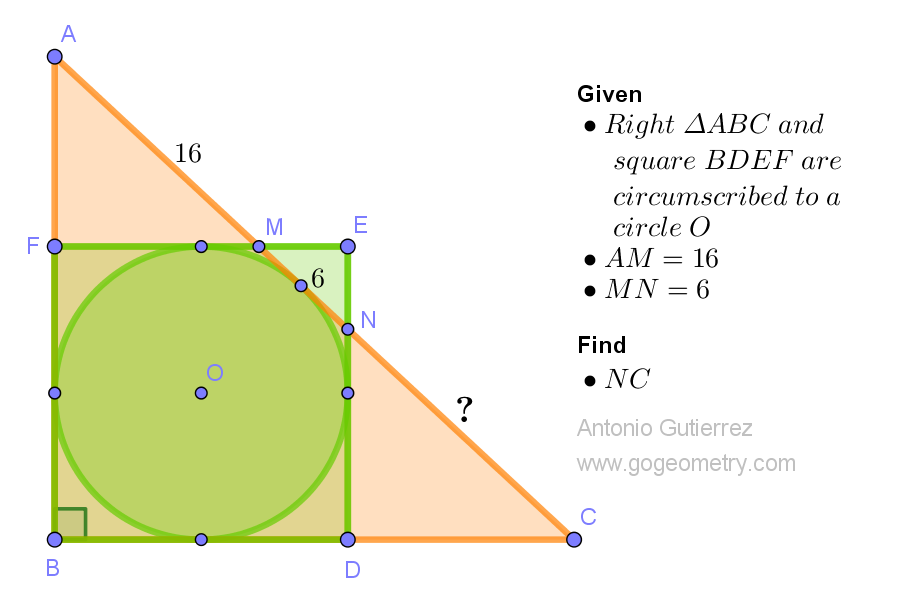
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
https://photos.app.goo.gl/9WJPkUonvmX8kLo5A
ReplyDeleteSee sketch for location of points P, Q,R and angles u, v and radius r
Note that triangles AFM, NEM and CDN are similar ( case AA)
And OM and ON are angle bisectors of angles POR and QOR= u+v= 45
We have ME/MF= MN/MA= 6/16 = ME/(2r- ME) => ME= 6/11. r
And PM= 5/11.r
tan(u+v)=( tan(u)+tan(v))/(1- tan(u).tanv))= 1,,,,, (1)
Replace tan(u)= PM/r= 5/11 in (1)
We get tan(v)=⅜= NQ/r => NQ= ⅜.r and NE= ⅝ . r and ND= 11/8 .r
We have NC/NM= ND/NE=(1.375 r)/(.625 r)= 11/5
So NC= 66/5
Let NC=x,
ReplyDeleteConsider triangle AOC,
Angle AOC=135 degrees,
Angle AOM = Angle MON = Angle NOC= 45 degrees,
ON is bisector of Angle MOC hence
OM/OC=MN/NC=6/x,
And OA is external bisector of Angle MOC, hence OM/OC=AM/AC=16/(x+22)
We get 6/x = 16/(x+22),
Simplifying it we get x=6×22/10=13.2 units.
NC = 11.2
ReplyDelete