Monday, May 15, 2023

Geometry Problem 1539: Unraveling the Lengths in an Isosceles Triangle with Altitude and Tangent Secrets!

Geometry Problem 1539. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.

Get the full picture! Click below to uncover the details.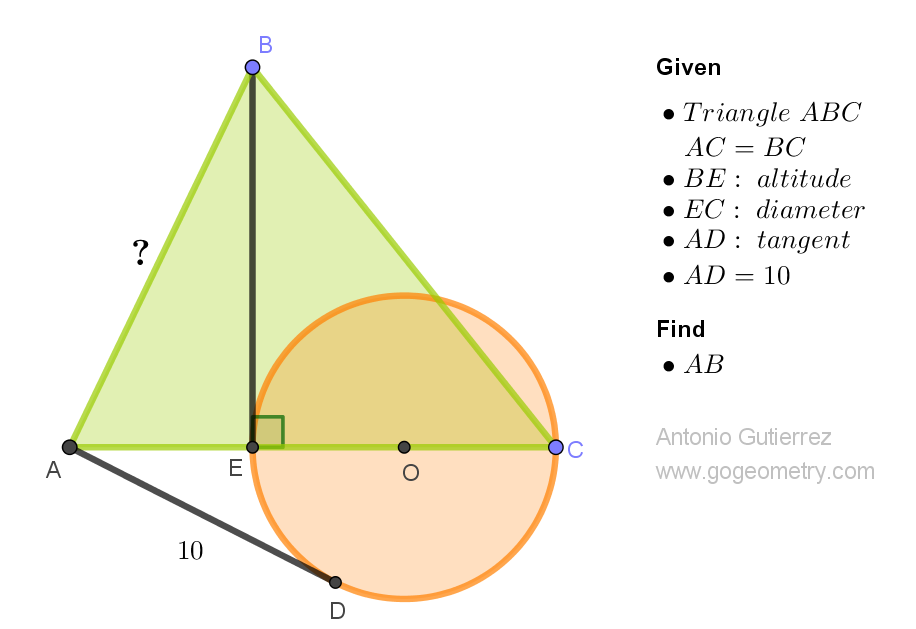

Geometry Problem 1539: Unraveling the Lengths in an Isosceles Triangle with Altitude and Tangent Secrets

Click for additional details.

Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.

Posted by Antonio Gutierrez at 4:46 PM
Labels: , , , , , , , ,

4 comments:

  1. Peter TranMay 15, 2023 at 9:37 PM

    https://photos.app.goo.gl/gmaVeeA2GEGK4kNd8

    Locate point F on AC extension such that AC=CF
    Note that ABF is a right triangle
    Power of point A to circle O = AE.AC= AD^2= 100
    Relation in right triangle ABF
    AB^2=AE.AF= 2.AE.AC= 200
    So AB= 10.sqrt(2)

    ReplyDelete
  2. Stan FULGERMay 17, 2023 at 10:19 AM

    If M is midpoint of AB, CBME is cyclic, thus AM.AB=AE.AC=AD^2, or AB^2=200, AB=10 sqrt (2)

    ReplyDelete
  3. AnonymousMay 18, 2023 at 9:47 PM

    Let M be midpint of AB.
    BCEM is concyclic.
    AM.AB = AE.AC = AD^2
    AB^2/2=100 => AB = 10 sqrt 2.

    ReplyDelete
  4. AnonymousMay 18, 2023 at 9:54 PM

    A more general version will be:
    AC = BC, BE is altitude, AD is tangent to a circle passing through E and C. Show that AB = AD sqrt 2

    ReplyDelete

Subscribe to: Post Comments (Atom)