Geometry Problem 1538. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Get the full picture! Click below to uncover the details.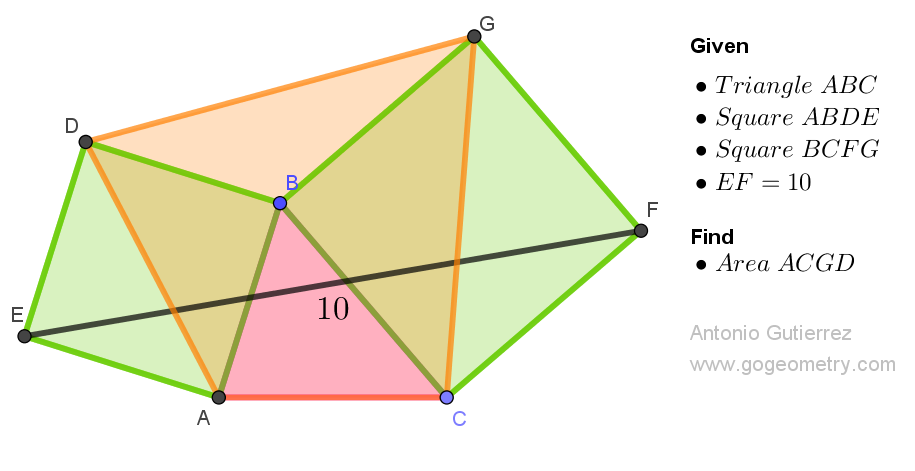
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Trigonometry Solution
ReplyDeleteS(ACGD) = C^2 /2 + a^2 /2 + (ac/2)SinB + (ac/2)Sin (180 - B)
S(ACGD) = (a^2 + c^2)/2 + (ac/2)sinB........(1)
EF^2 = 2c^2 + 2a^2 - 2(V2a)(V2c)cos(90+B)
EF^2 = 4{(a^2 + c^2) + (ac/2)sinB}......(2)
From (1) & (2),
S(ACGD) = EF^2 / 4 = 10^2 / 4 = 25
Sumith Peiris
Moratuwa
Sri Lanka
Some clarifications and correcting of typos
DeleteS(AGCD) is the sum of areas of Triangles ABD, DGB, CBG & ABC
Equation (1) should be corrected to read as
S(ACGD) = (a^2 + c^2)/2 + ac.sinB......(1)
The length of EF is obtained by applying the Cosine Rule to Triangle EBF
Equation (2) should be corrected to read as
4{(a^2 + c^2)/2 + ac.sinB}................(2)
RHS of (2) is 4 times RHS of (1)
A slightly different version of Stan's excellent geometry proof.
ReplyDeleteLet AG,CD meet at P
Triangles ABG & CBD are congruent SAS, so AG = CD......(1)
Also since < AGB = < BCD, BPCG is concyclic and so EF^2 =2. AG^2 = 2. 2. S(ACGD) from (1)
So S(AGCD) = EF^2 / 4 = 10^2 / 4 = 25
Sumith Peiris
Moratuwa
Sri Lanka