Geometry Problem 1529. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.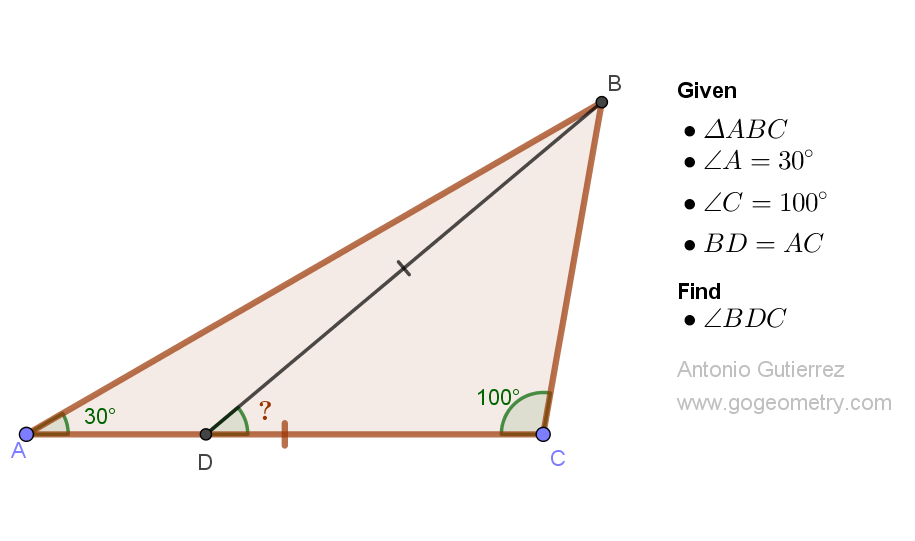
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Trigonometry Solution
ReplyDeleteLet < BDC = y
In Triangle ABC, a/sin30 = b/sin50 ...............(1)
In Triangle BDC, a/sin.y = b/ sin100.............(2)
(1)/(2); sin.y/ (1/2) = sin100/sin50 = 2cos50
So sin.y = cos50 = sin40
Hence y = 40 = < BDC
Sumith Peiris
Moratuwa
Sri Lanka
Geometry Solution
ReplyDeleteLet O be the Circumcentre of Triangle ABC. C being obtuse, O is outside the Triangle. Drop a perpendicular OX to CO extended. Drop a perpendicular BY to AC extended.
< COB = 2 X 30 = 60 so Triangle BCO is equilateral. < AOC = 2 X < ABC = 100, < ACO = 40 since Triangle ACO is isosceles
Triangles AOX & BCY are congruent ASA and so AX = BY
Hence Triangles ACX & BDY are congruent (Hypotenuse, side, 90)
Therefore <BDC = ACX = 40
Sumith Peiris
Moratuwa
Sri Lanka
Similar to previous.
ReplyDeleteLet O be circumcenter of ABC.
BOC is equilateral.
OAC is a 100-40-40 triangle.
OAC and CBD has two equal sides and one equal angle.
This means either BDC = ACO or BDC = 180-ACO.
Second one violates triangle conditions.
So OAC is similar CBD. So angle BDC = 40.