Monday, March 6, 2023

Geometry Problem 1521: Unlock the Secret to Finding the Measure of an Angle in a Triangle with Two Sides as Diameters of Circles. Difficulty Level: High School.

Geometry Problem 1521. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.

Details: Click on the figure below.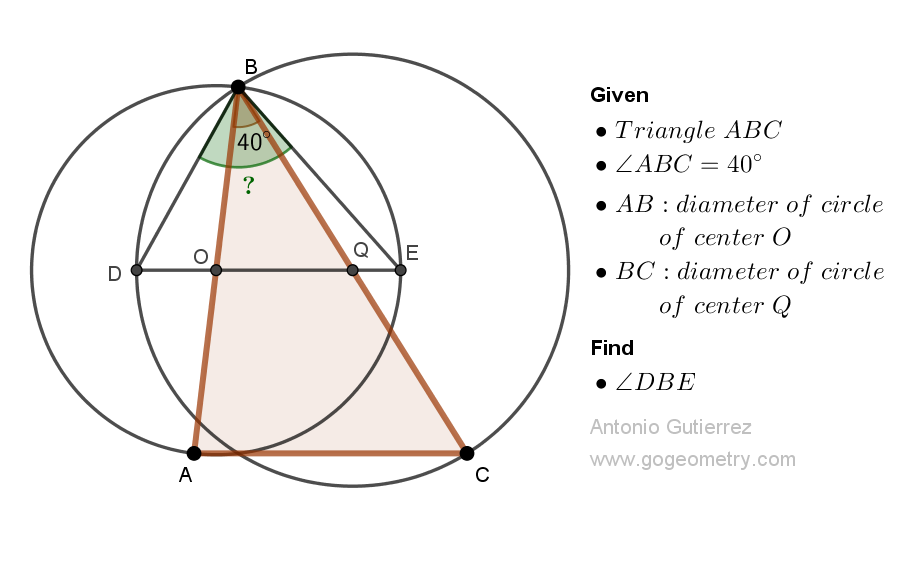

Geometry Problem 1521: Unlock the Secret to Finding the Measure of an Angle in a Triangle with Two Sides as Diameters of Circles. Difficulty Level: High School.

More Details

To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.

Posted by Antonio Gutierrez at 12:11 PM
Labels: , , , , , ,

5 comments:

  1. c.t.e.o.March 6, 2023 at 1:26 PM

    DBE = 70° (It will be explained on the sketch)

    ReplyDelete
    Replies
    1. c.t.e.o.March 7, 2023 at 10:01 AM

      https://photos.app.goo.gl/KzkMvaHgbfKy5cqt7

      Delete
    2. c.t.e.o.March 24, 2023 at 5:01 PM

      Again one comment is deleted : https://photos.app.goo.gl/CxQ2Xvm1BvtF8zg19

      Delete
  2. Sumith PeirisMarch 6, 2023 at 3:14 PM

    Let <QBD = < QDB = p and let < OBE = < OEB = q

    In Triangle OQB,
    (p+p-40) + (q + q - 40) = 140
    So p + q = 220/2 = 110

    Hence < DBE = p + q - 40 = 70

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete
  3. Peter TranMarch 6, 2023 at 7:22 PM

    https://photos.app.goo.gl/kYPKJjPWmLn4TNQd7

    Note that BOE and BQD are isosceles triangles
    See sketch for angles d, o, q and e
    We have d= 90-½.q
    And e=90-½. o
    So d+e= 180-½(q+o)
    But q+o= 180- ∡(ABC)= 140
    So d+e= 110
    And∡(DBE)= 180-(d+e)= 70

    ReplyDelete

Subscribe to: Post Comments (Atom)