Geometry Problem 1522. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.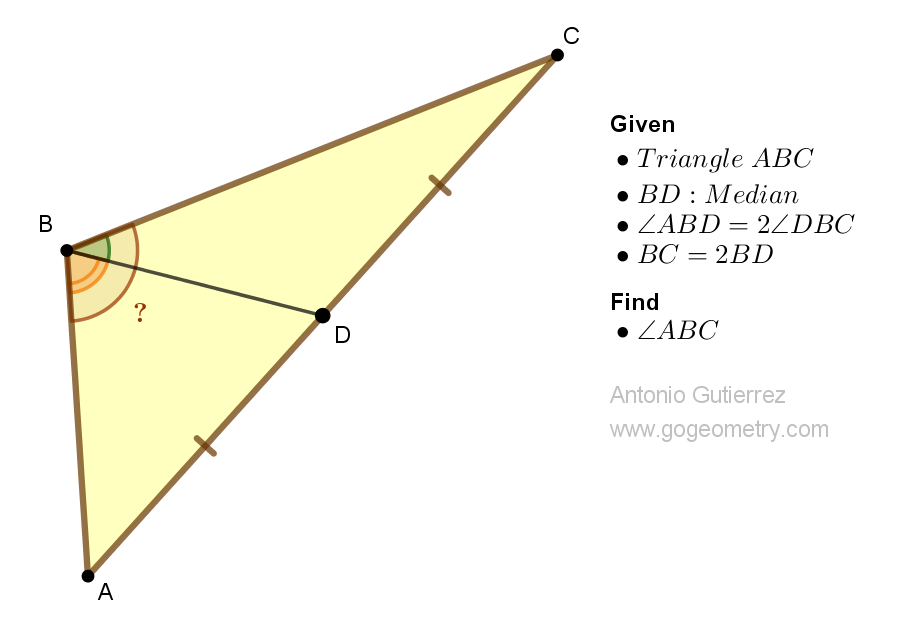
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Let E be the mid point of BC. Let <DBC = @ so that < ABD = 2@
ReplyDeleteNow BE = EC = BD
So Triangle BDE is isosceles and <BED = <BDE = 90 - @/2
From the midpoint theorem for Triangle ABC,
DE//AB so < ABD = 2@ = < BDE = 90 - @/2
Hence 5@/2 = 90 and so @ = 36
Therefore < ABD = 2@ = 72
Sumith Peiris
Moratuwa
Sri Lanka
< ABC = 3@ = 108
DeleteBD/BC = AD/AC = 1/2 implies BA is the (external) angle bisector of DBC.
ReplyDelete2a+2a+a=180, a=36, ABC = 3a = 108.
Angle ABC=108 degree
ReplyDelete