Geometry Problem 1520. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.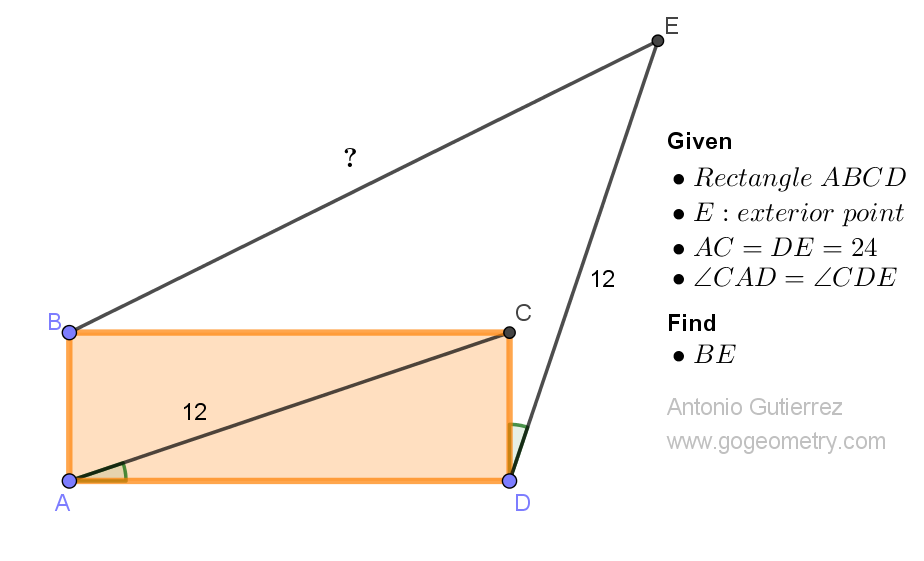
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
12V2 (V2 = sqrt of 2)
ReplyDeleteComplete Right Triangle BEF, F on BC extended.
ReplyDeleteComplete Right Triangle DEG, G on DC extended.
Let AD = a and CD = b
Triangles DEG & ACD are congruent ASA
So GE = b = CF and hence EF = a - b and BF = a + b
So in Triangle BEF,
BE^2 = BF^2 + EF^2 = (a+b)^2 + (a-b)^2 = 2 (a^2 + b^2) = 2 AC^2 = 2 X 12^2
Therefore BE = 12. sqrt2
Sumith Peiris
Moratuwa
Sri Lanka
Connect B and D then <BDE=90⁰
ReplyDeleteBE² = BD² + DE²
BE² = 12² + 12² = 12 ROOT2