Geometry Problem 1510. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.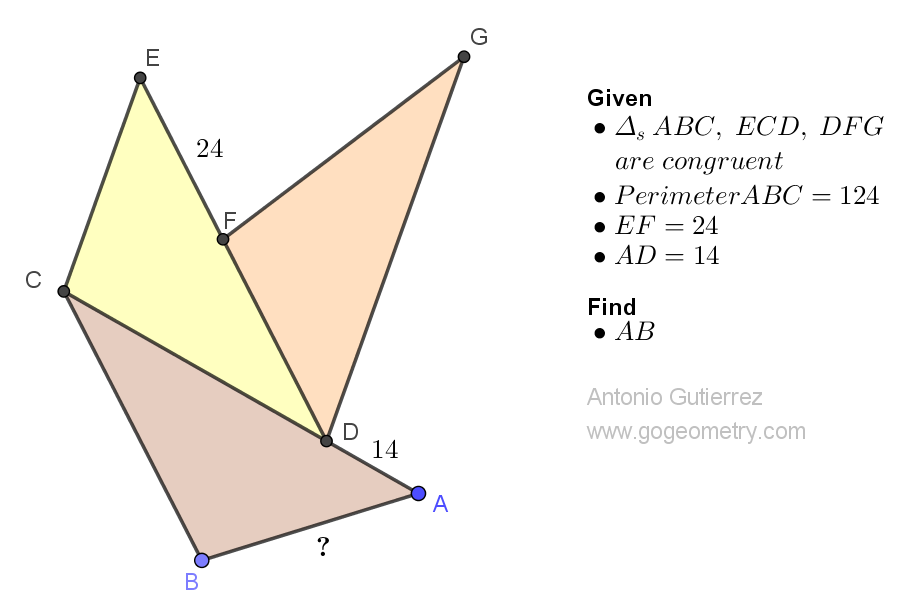
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Let AB = c, BC = a and AC = b
ReplyDeleteThen CD = a = b - 14.......(1)
Also DF = c = b - 24........(2)
We are given that a + b + c = 124 .......(3)
(1) + (2) + b we get a + b + c = 3b - 38 = 124 from (3)
So 3b = 162 and b = 54
From (2) AB = c = b - 24 = 54 - 24 = 30
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/NMEUvbczc1FiduxB7
ReplyDeleteLet a, b, c are 3 sides of triangle ABC
Per sketch attached we have
b-a= 14 ….(1)
b-c=24…(2)
a+b+c= 124 ….(3)
From (1) and (2) we have b= c+24 and a=c+10
Replace it in (3) we have c= 30, a=40 and b=54
So AB= c= 30
Let AB be x, BC be y, and AC be z
ReplyDeletethen we know that x + y + z = 124
then by substitution we know that x + y + y + 14 = 124 since z = y + 14
We also know that x + x + y + 24 = 124 since y = x + 24
If we simplify these formulas we know that 2x + y = 100 and x + 2y = 110
Finally we use elimination to solve this equation and get x = 30