Geometry Problem 1509. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.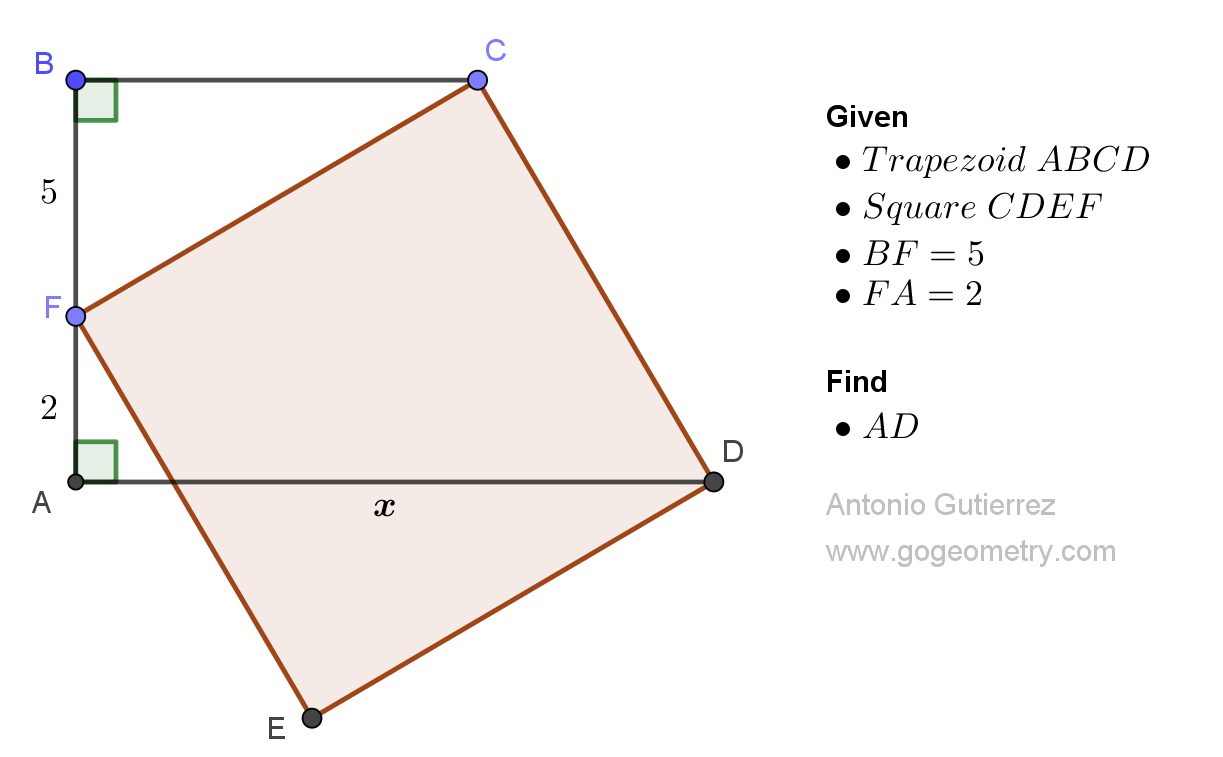
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Extend FB to point G such that BF=BG. Then we get CF=CG=CD, hence C is center of circle passing through points D,F and G. Since Angle DCF=90, Angle DGF=90/2=45.
ReplyDeleteHence Triangle ADG is right isosceles. We get AD=AG=AF+BF+BG=2+5+5=12.
Very elegant solution Pradyumna, much better than my own
DeleteThank you Sumith for your kind comment.
DeleteExtend CF to G
ReplyDeleteLet the side of the square be a, let GF = t and AG = q
From similar triangles BCF, AGF and GCD
5/a = 2/t = a/(q+x).....(1)
Since AFCD is concyclic, t(a+t) = q(q+x)....(2)
Substituting from (1) (2a/5)(a+2a/5) = (a^2/ 5 - x)(a^2/ 5)
14/5 = a^2/ 5 - x and a^2 = 14 + 5x...(3)
But x^2 +2^2 = 2.a^2
Therefore x^2 + 4 = 28 + 10x from (3)
x^2 - 10x - 24 = 0
(x+2)(x-12) = 0
So x = 12 since x = -2 is not permissible
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/tM61SHQ3HgmUEZrp9
ReplyDeleteLet H is the project of C over AD
Note that triangle FBC congruence to DHC ( case AA)
So HD=BF=5 and CH=AB=7
So AD=12
Good solution, Peter
DeleteThank Sumith
Deletec.t.e.o.https://photos.app.goo.gl/4E2MnjC9GN6Xd7fz9
ReplyDeletehttps://photos.app.goo.gl/4E2MnjC9GN6Xd7fz9
ReplyDeleteAnother Solution.
ReplyDeleteComplete Rectangle ADYX.
Then Triangle BCF, XFE and YED are congruent ASA.
So XE = DY = FB = 5 and hence, FX = EY = 7. Therefore AD = XE + EY = 5 + 7 = 12
Sumith Peiris
Moratuwa
Sri Lanka
Note that E is on XY
Delete