Geometry Problem 1501. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.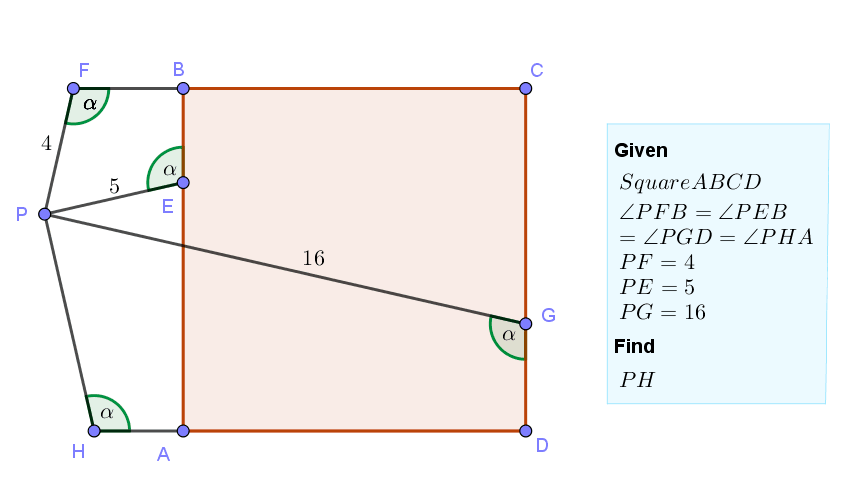
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Let PG and AB intersect at point K.
ReplyDeleteThen Angle PKA= Angle PGD =Alpha.
Hence Triangle PKE is isosceles with PK=PE.
Extend FP to meet line DA at point L. We have isosceles Triangle PLH with PL=PH.
FL=PF+PL=PF+PH
Also FL=GK (since both segments make equal angle with side of square FL.sin(180- Alpha)=GK.sin(180-Alpha)=side of square)
We get PG=GK+PK=FL+PE=PF+PH+PE
16=4+5+PH, we get PH=7.
https://photos.app.goo.gl/JC82i2iPQsHZMMC26
ReplyDeleteCalculate PM= PG.sin (a)= 16.sin(a)
PN= PEsin(a)=5.sin(a)
PU=PF.sin(a)= 4 sin(a)
PV= PH.sin(a)
Since ABCD is a square => PU+PV=PM-PN
So PV= 7.sin(a) => PH= 7
Let FP, DH extended meet at V
ReplyDeleteLet PG, AB meet at U
Drop a perpendicular UX to CD, X on CD
Complete rectangle CDVW
PE = PU = 5
Tr.s VWF & GUX are congruent ASA
So FV = UG = 11
Hence PV = 11- 4 = 7
But PV = PH
Hence PH = 7
Sumith Peiris
Moratuwa
Sri Lanka