Geometry Problem 1502. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.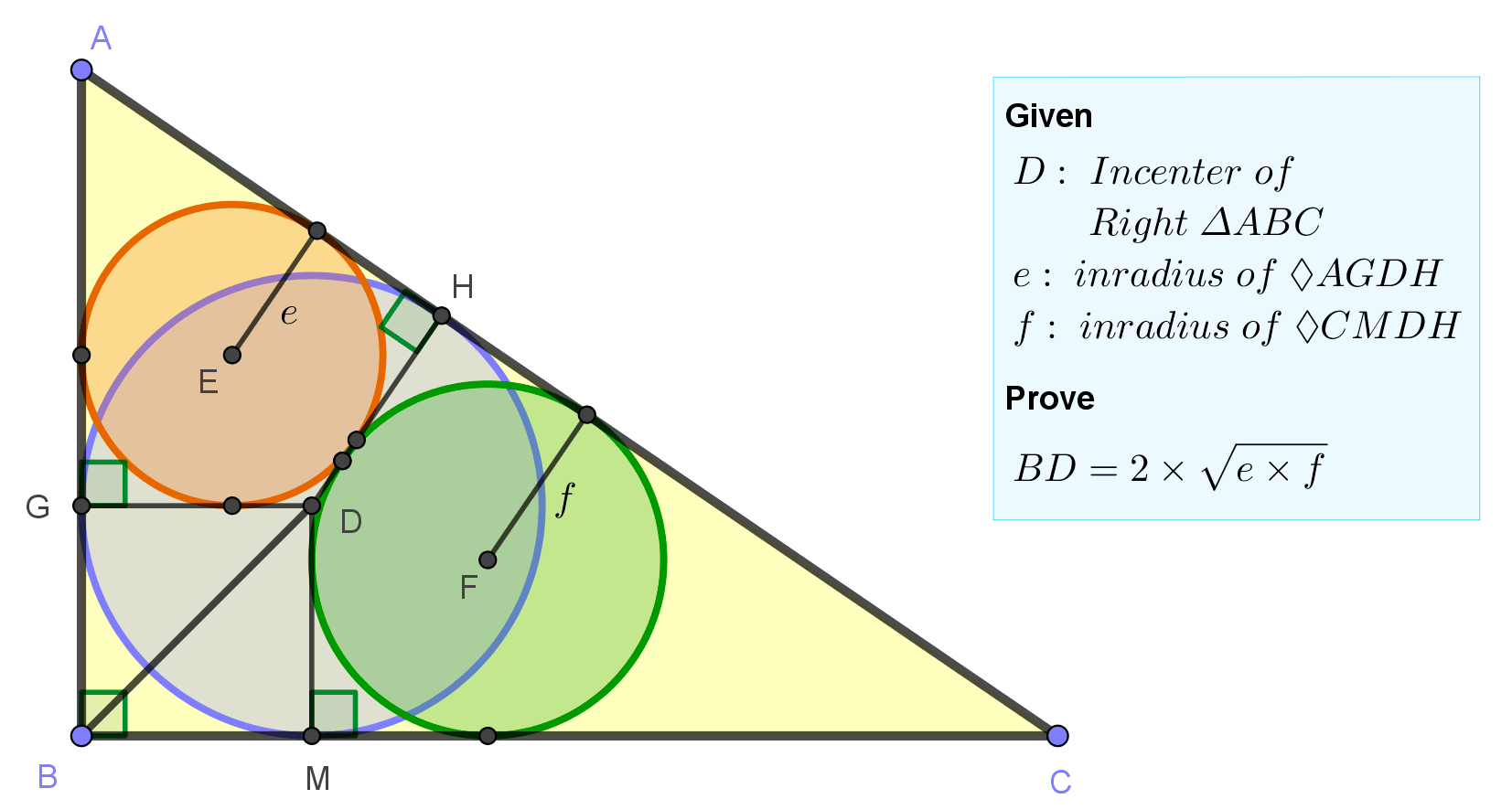
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
If the inradius of Tr. ABC = r and the semi perimeter = s,
ReplyDeleteThen r = S(ABC)/s = (ac/2) / [(a+b+c)/2) = (a+c - b)/2 = s-b ....(1)
Now A,E,D are collinear so from similar Tr.s, e/r = (s-a-e)/(s-a) = (s-a)/(r+s-a)
So e = (s-b)(s-a)/c ....(2) since r+s-a = c where we have used r = s-b from (1)
Similarly f = (s-b)(s-c)/a ....(3)
(2) X (3) gives e.f = (s-b)^2 . (s-a)(s-c)/ac
e.f = (s-b)^2 (b+c-a)(b+a-c)/(4ac) = (s-b)^2. {b^2 - (c-a)^2}/(4ac) = (s-b)^2 / 2
(since a^2 + c^2 = b^2)
Now BD^2 = 2.r^2 = 2(s-b)^2 from (1)
Hence BD^2 = 4ef and the result follows
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/46pkyTFQ4edo5UjX8
ReplyDeletelet a, b, c are sides of triangle ABC with perimeter 2p and inradius r
let DG and DM cut AC at P and Q ( see sketch)
Note that f and e are inradius of triangles QMC and AGP
and triangles QMC and AGP are similar to triangle ABC
Note that ration of inradius of 2 similar triangles will be ratio of 2 triangles
We have CM= p-c= (a+b-c)/2 and AG=p-a = (-a+b+c)/2
so f/r= CM/CB= (a+b-c)/2a
and e/r=AG/AB= (-a+b+c)/2c
so (e.f)/(r.r)= (-a+b+c) x( a+b-c)/(2a.2c)= (b^2-(a-c)^2)/(4ac)....... (1)
replace b^2=a^2+c^2 in (1) and simplify we get
(e.f)/(r.r)= 1/2 and the result follow