Geometry Problem 1497. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.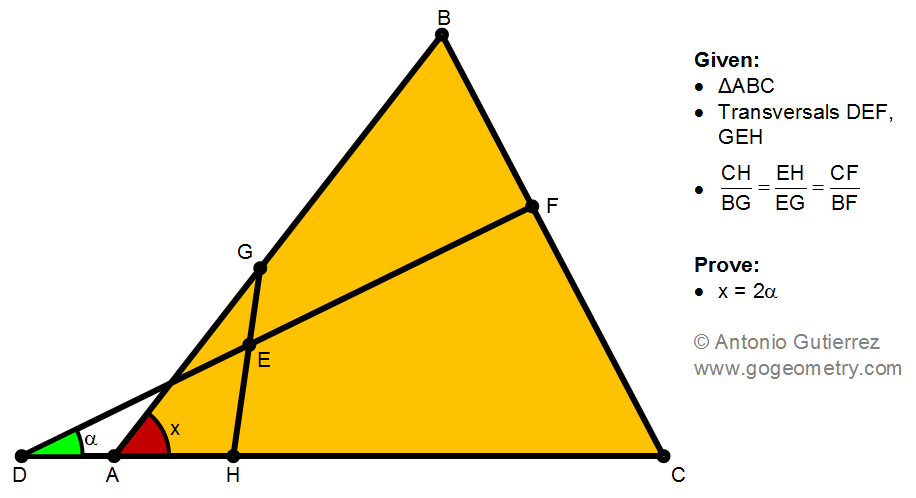
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Where is Problem 1496?
ReplyDeleteLink: https://gogeometry.com/school-college/5/p1496-triangle-double-angle-isosceles-30-degree-congruence.htm
DeleteTo Antonio : I published solution for this problem few weeks ago . The solution appear in few days then disappear later. I am not sure if there are something wrong in my solution ?
ReplyDeletePeter Tran has left a new comment on your post "Geometry Problem 1497: Scalene Triangle, Transversal, Same Ratio, Proportionality, Isosceles, Double Angle":
Deletehttps://photos.app.goo.gl/vwzCfb5NrWeMwChR6
Problem 1497 solution 2
Draw GK//HC
C, E and K are collinear points => triangles HEC similar to GEK ( case AA)
We have EH/EG=HC/GK=CE/CE => BG=GK
Let BK meet DC at L
Since EH/EG=CE/EK= CF/FB=> BK//EF ( Thales theorem)
We have isosceles and similar triangles GBK and LAB ( case AA)
And ∠ (ALB)= ∠ (ABL)= ∠ (FDC)=alpha
And x= ∠ (HAG)= 2. Alpha
Peter Tran has left a new comment on your post "Geometry Problem 1497: Scalene Triangle, Transversal, Same Ratio, Proportionality, Isosceles, Double Angle":
ReplyDeletehttps://photos.app.goo.gl/LcWs7W3YV9TyGRYW8
Draw BK//HC
H, F and K are collinear points => triangles HFC similar to KFB ( Case AA)
We have CF/BF=HF/FK=CH/BK=CH/BG => BG=BK
Let GK meet DC at L
Since EH/EG=CF/BF=HF/FK => GK//EF ( Thales theorem)
We have isosceles triangles GBK and LAG
And ∠ (ALG)= ∠ (AGL)= alpha
And x= ∠ (HAG)= 2. alpha
Posted by Peter Tran to Go Geometry (Problem Solutions) at Sep 17, 2022, 7:28 PM
My solution, given by the construction of the points E,F may be found at my blog : https://stanfulger.blogspot.com/2022/11/problem-1497-go-geometry.html
ReplyDeleteBest regards,
Stan Fulger