Geometry Problem 1496. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.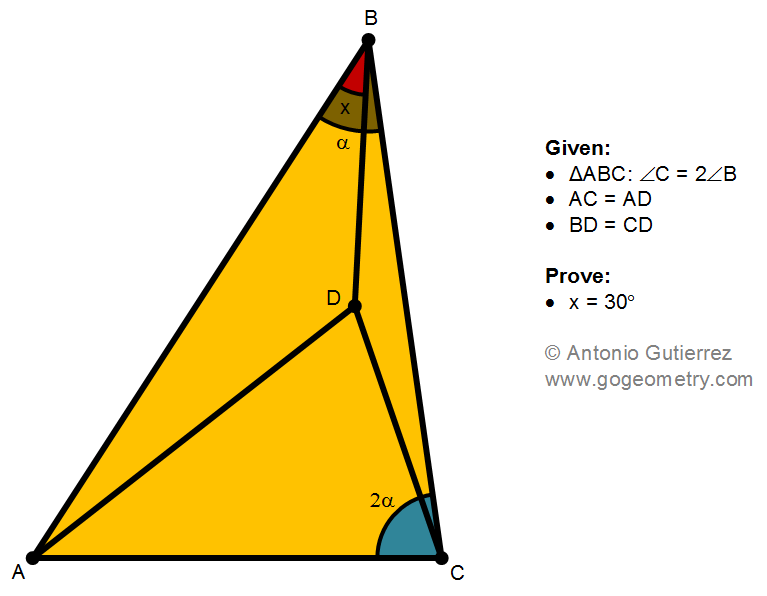
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Trigonometry Solution
ReplyDelete<BCD = <CBD = @ - x
<ADC = < ACD = @ + x
Let BD = CD = d
Now write the Sine Formula for Tr.s BCD, ACD, ABC noting that sin (180 - p) = sin p and that sin 2q = 2.sin q. cos q
a/d = sin [2(@ - x)] / sin(@ - x) = 2.cos(@ - x).........(1)
d/b = sin [2(@+x)] / sin(@-x) = 2.cos(@+x)............(2)
a/b = sin 3@ / sin @ ................................................(3)
(1) X (2) ;
a/b = 4.cos (@-x).cos (@+x) = 4.(cos @.cos x + sin @. sin x).(cos @.cos x - sin @.sin x)
a/b = 4.(cos^2 @. cos^2 x - sin^2 @. sin^2 x) (difference of 2 squares)
= 4.[(1 - sin^2 @). (1 - sin^2 x) - sin^2 @. sin^2 x) since sin^2 w + cos^2 w = 1
= 4. (1 - sin^2 @ - sin^2 x)
= 3 - 4.sin^2 @ from (3)
So 4. sin^2 x = 1
and sin x = 1/2 and x = 30
Sumith Peiris
Moratuwa
Sri Lanka
Geometric Solution:
ReplyDeleteLet point E be the middle point of BC. Since BD = CD, therefore ED is the perpendicular bisector of BC.
Extend ED and let it intersect AB at point F. Hence BF = CF and <FBC = <FCB = \alpha.
Therefore triangulars ABC and ACF are similar, and AB * AF = AC^2.
Since AD = AC, thus AB * AF = AD^2, therefore triangulars ABD and ADF are similar, and <ADF = <ABD = x.
Finally, since <EDC = 90 - \alpha + x, and <CDA = \alpha + x, and <ADF = x,
therefore, 180 = <EDF = <EDC + <CDA + <ADF = 90 + 3*x, and we conclude x = 30.
Q.E.D.
Very good. I got as far as BF=BC but failed to realize that <ADF =x
ReplyDeleteTake E on BC so that BE=AE=AC, <AEB=180-2a, take then reflection of E about AB, see that ACBF is an isosceles trapezoid and BF=AF=DF=AD, triangle ADF is equilateral, F is the circumcenter of triangle ADF, thus the required angle is 30 degs!
ReplyDeleteSe ubica E exterior y relativo a AB tales que:medida del angulo EBC sea 2alpha y EB=AC ,luego:EB=ED=EA.Finalmente x=30°
ReplyDelete