Challenging Geometry Puzzle: Problem 1572. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.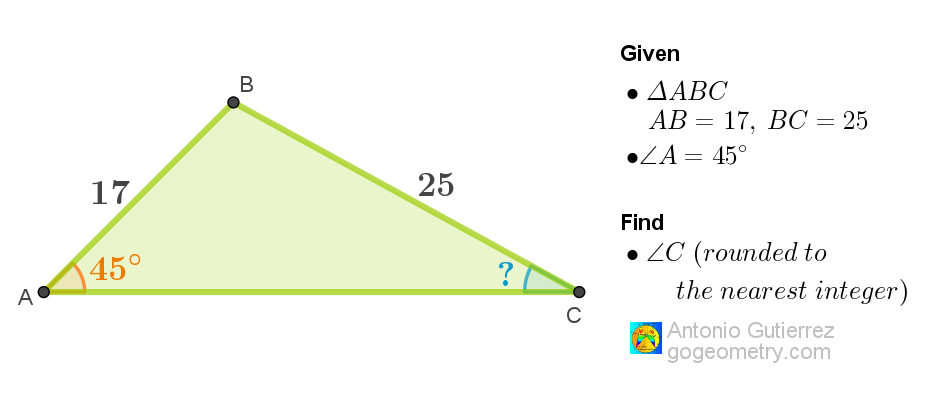
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
the problem want us to use geometric methods rather than trigonometry to enhance understanding of the triangle's properties.
ReplyDeleteDraw a 7-24 -25 Right Triangle BCE with BE = 24, CE = 7 and BC = 25
ReplyDeleteSo CE // AB and hence CDE & ABD are both right isosceles
From Problem 1571, < BCE = 74 and so
< C = 74 - 45 = 29
Sumith Peiris
Moratuwa
Sri Lanka
A better Pure Geometry proof
ReplyDeleteDraw BD perpendicular to AB, D on AC. Draw CE // AB, E on BD extended
Now both Triangles ABD & CDE are right isosceles
Let CE = DE = x
Using Pythagoras in Triangle BCE,
x^2 + (x + 17)^2 = 25^2
So we have a quadratic equation in x
2x^2 + 34x - 336 = 0, from which
x = 7 or x = -24 which root can be disregarded
So x = 7 and CDE is a 7-24-25 Right Triangle with < BCE = 74 from Problem 1571
Therefore <C = 74 - 45 = 29
Sumith Peiris
Moratuwa
Sri Lanka