Challenging Geometry Puzzle: Problem 1565. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.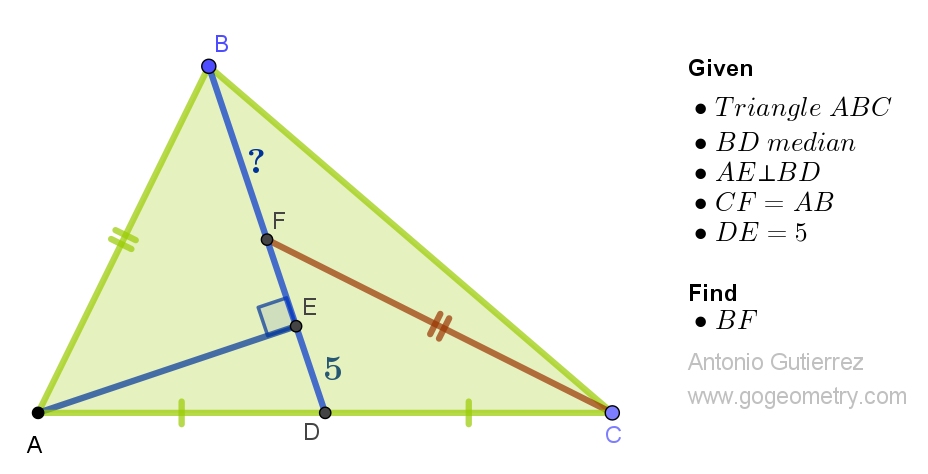
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Extent BD=DG. Draw CH┴DG (H on DG)
ReplyDeleteTrABD, TrCGD are congruence (SAS) so GC=AB=CF,<ABD=<G
TrEAB,TrHCG are congruence (Right Triangles, CG=AB,<ABE=<G) so
BE=HG but HG=HF (TrCGH=TrCFH) so BE=HF
BE=HF → BF+EF=EF+EH → BF=EH=5+5=10 (EH=2ED)
On the line BD take a point G symmetric to B relative to D, so that DG = BD. Then triangle DGC is congruent to ABD (AD = DC, BD = DG, angle <BDA = <CDG, SAS case). Project point C to the line BDG, and call it H. As AD = DC, <EDA = <CDH,
ReplyDeleteso DH = ED = 5.
Also HG = BE, because ABE and CGH are right triangles, angle <ABE = <CGH and CG = AB.
Now, CF = AB (by hypothesis) and CG = AB (congruence of triangles ABD and DGC as seen before), implies that CF = CG and triangle FCG is isosceles. Then H is the middle point of FG, so that FH = HG, and as we saw HG = BE, and then FH = BE.
But,
FH= FE + ED + DH = FE + 5 + 5 = FE + 10;
BE = BF + FE,
So FH = BE implies FE + 10 = BF + FE, and cancelling FE we obtain BF = 10.
Joaquim Maia
Rio de Janeiro
Brazil
Extend ED to X such that D is the midpoint of EX
ReplyDeleteThen AECX is a parallelogram and AE = CX
Hence Triangles ABE & CFX are congruent (Hypotenuse, side, right angle)
So BE = FX, hence BF = EX = 10
Sumith Peiris
Moratuwa
Sri Lanka