Challenging Geometry Puzzle: Problem 1559. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.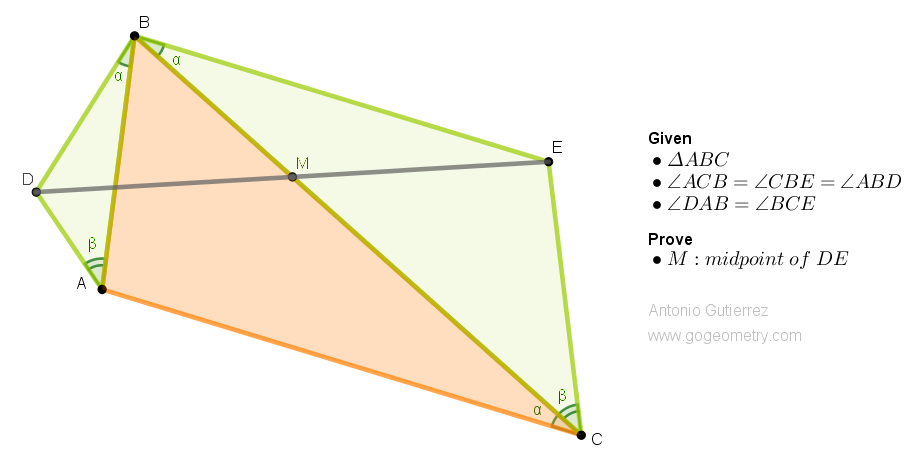
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Let CA and BD extended meet at F. Draw FG // DE, G on BE extended.
ReplyDeleteLet FG and BC cut at N. Extend AC to L
Let FD = u, DB = v, AD = w
Let BE = x, EG = y , CE = z
Since DE//FG, v/u = x/y........(1)
Since Triangles ABD and BCE are similar
v/w = x/z...............(2)
From (1) and (2) x/v = y/u = z/w ..........(3)
Now in Triangles ADF & CEG from (3)
u/w = y/z and the included angles < ADF = < CEG (= alpha+beta)
Hence Triangles ADF & CEG are similar & < AFD = < CGE = < GCL since CF // BG
So BFCG is a parallelogram and the diagonals bisect each other
Hence BN bisects FG and since FG//DE, BN (or BM) also bisects DE
Sumith Peiris
Moratuwa
Sri Lanka
Draw line DN //BE and connect E TO N on INTERSECTION DN TO BC . And INTERSECTION BA AND DN is S. We can prove BEND is parallelogram BE=X BD=V EN=L EC=S DA=K NC=R SA=P Triangles BDA AND BEC are similar so X/V=S/K=R/P In Triangle BAC R/P=T/U SO T/U=R/P=S/K=X/V it prove that Triangles BEN and BDS are similar & <BDN=<BEN SOBEDN IS parallelogram and the diagonals bisect each other. BEHROUZ L.A.
DeleteI think the problem would have been more difficult if it required to prove that AB is symmedian of triangle BDE
ReplyDelete