Sunday, October 29, 2023

Geometry Problem 1558: Three Equilateral Triangles

Challenging Geometry Puzzle: Problem 1558. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.

Gain comprehensive insights! Click below to reveal the complete details.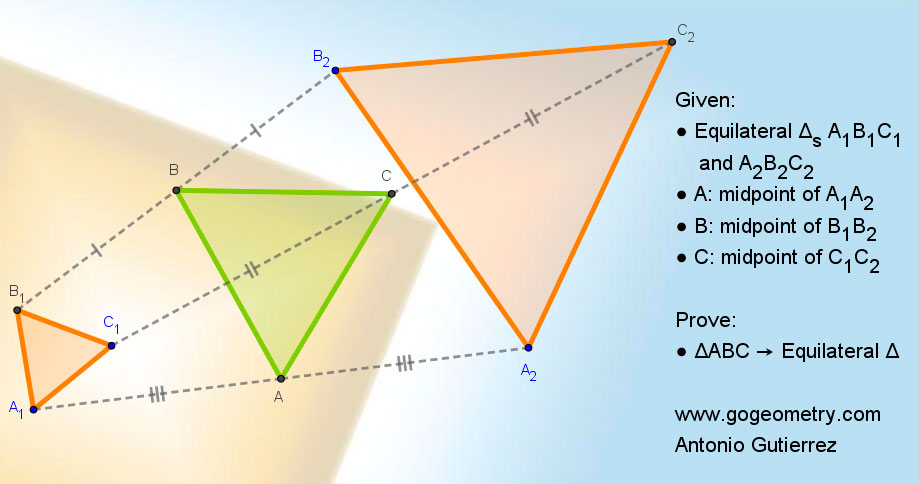

Illustration of Geometry Problem 1558: Three Equilateral Triangles

Click for additional details.

Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.

Posted by Antonio Gutierrez at 7:48 PM
Labels: , , ,

6 comments:

  1. Sumith PeirisNovember 13, 2023 at 10:11 PM

    Perpendiculars from C1, C and C2 to B1B2 (extended to R) meet B1B2 at P, Q and R respectively.
    Let C1B1= a and CB2 = b.
    Let B1P = t1, PB = t2, BQ = t3, QB2 = t4 and B2R = t5.
    Let C1P = u and C2R = v

    C1PRC2 is a trapezoid with C1P//CQ//C2R, so by connecting C2P and applying the midpoint theorem,
    CQ = (u+v)/2 ..........(1) and
    t2 + t3 = t4 + t5 ......(2)
    Now it is given that t1 + t2 = t3 + t4....... (3)
    From (2) and (3), t3 = (t1 + t5) / 2..........(4)

    Now consider Right Triangles B1C1P, BCQ and B2C2R
    CQ = (u + v)/2
    BQ = t3 = (t1+ t5)/2
    and the included angle is 90

    So BC = (a + b)/2
    Similarly we can show that CA = (a+b)/2 and AB = (a+b)/2

    Therefore Triangle ABC has BC = CA = AB and is thus equilateral

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete
  2. César Eliud LozadaMay 19, 2024 at 4:50 PM

    This is not true if A1B1C1 and A2B2C2 have opposite orientations.

    ReplyDelete
  3. AnonymousJuly 3, 2024 at 6:30 AM

    Extend A2B to C3 so that A2B=BC3. Then B1C3=A2B2 and AB=A1C3/2. In the same way, B2C=CA3 and C2A=AB3. Triangle A2B3C3 is equilateral, so is ABC.

    ReplyDelete
  4. AnonymousJuly 5, 2024 at 7:50 AM

    I do not undertand why BC=(a+b)/2

    ReplyDelete
    Replies
    1. AnonymousJuly 6, 2024 at 4:13 AM

      If A1B1 is parallel to and has the same orientation with A2B2, then BC=(a+b)/2. But then the problem is trivial. For the general case see previous comment.

      Delete
  5. AnonymousJuly 21, 2024 at 9:42 AM

    It is possible to solve this problem using complex numbers. Label the points A1 as ZA1 (A1 as complex vector), A2 as ZA2, and so on. By the figure and the hypothesis that A1B1C1 and A2B2C2 form equilateral triangles, we find,
    (ZC1- ZA1)*cis 60º = ZB1 - ZA1, and (ZC2 - ZA2)*cis 60º = ZB2 - ZA2. Summing term by term these equations and dividing both by 2, we have:
    ((ZC1 + ZC2)/2 - (ZA1 + ZA2)/2)*cis 60º = (ZB1 + ZB2)/2 - (ZA1 + ZA2)/2 (1)
    But, (ZC1 + ZC2)/2 = ZC, (ZA1 + ZA2)/2 = ZA and (ZB1 + ZB2)/2 = ZB, replacing in (1) we get,
    (ZC - ZA)*cis 60º = ZB - ZA, which means that ABC forms an equilateral triangle.

    Observe that this solution depends exactly on the orientations of the triangles A1B1C1 and A2B2C2, reinforcing the comment of Mr. César Eliud.

    Joaquim Maia
    Rio de Janeiro
    Brazil

    ReplyDelete

Subscribe to: Post Comments (Atom)