Saturday, September 9, 2023

Geometry Problem 1552: Exploring Angle C in Triangle ABC with Given Angle A and Side Lengths

Challenging Geometry Puzzle: Problem 1552. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.

Gain comprehensive insights! Click below to reveal the complete details.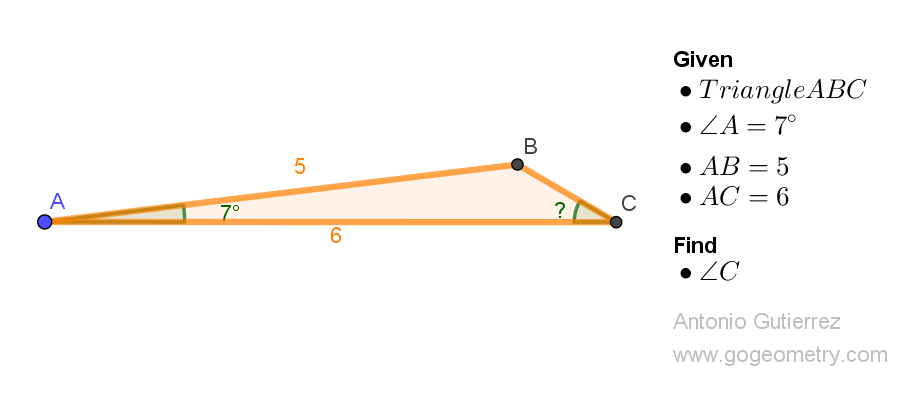

Illustration of Problem 1552: Exploring Angle C in Triangle ABC with Given Angle A and Side Lengths

Click for additional details.

Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.

Posted by Antonio Gutierrez at 5:41 PM
Labels: , , , ,

3 comments:

  1. Sumith PeirisSeptember 18, 2023 at 5:53 AM

    Trigonometry Solution

    Let < BCA = x

    Then by the Sine Rule for Triangle ABC
    sin(x+7)/sinx = 6/5 = 1.2
    sin7 + cos7. cot x = 1.2
    tanx = sin7/(1.2 - cos7) = 0.5814
    x = 30.43 degrees

    If there is a pure geometry solution I would love to see it

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete
  2. AnonymousFebruary 22, 2025 at 2:55 PM

    x = 30° Construir el triángulo equilátero APC, hacia el mismo lado que B. Trazar BH perpendicular a AP. Luego, los triángulos ABC y PBC son congruentes (LAL): c = 30°

    ReplyDelete
    Replies
    1. Sumith PeirisFebruary 24, 2025 at 4:58 PM

      English translation the above proof

      x = 30° Construct the equilateral triangle APC, on the same side as B. Draw BH perpendicular to AP. Then, triangles ABC and PBC are congruent (SAS): c = 30°

      Triangles ABC and PBC are not congruent

      Delete

Share your solution or comment below! Your input is valuable and may be shared with the community.

Subscribe to: Post Comments (Atom)