Challenging Geometry Puzzle: Problem 1553. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.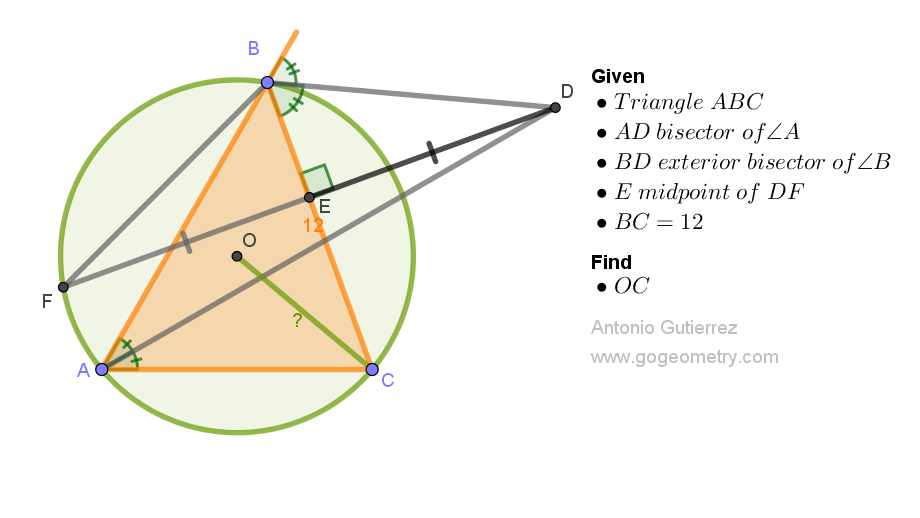
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
D is the Excentre of Triangle ABC
ReplyDeleteSo < EBD = (180-B)/2 and < BDE = B/2 = < BFE (since BEC perpendicularly bisects DF)
Similarly < CDE = C/2 = <CFE
Adding, < BFC = (B+C)/2 = < BAC = A
So B + C = 2A, hence A+B+C = 3A = 180 and A = 60
Area of Triangle ABC, S = abc/ 4R ................(1) (R = circumradius)
But also S = (1/2)bc.sinA = (bcV3)/4 = abc/4R from (1)
Therefore R = a/V3 = 12/V3 = 4V3
Sumith Peiris
Moratuwa
Sri Lanka