Challenging Geometry Puzzle: Problem 1550. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.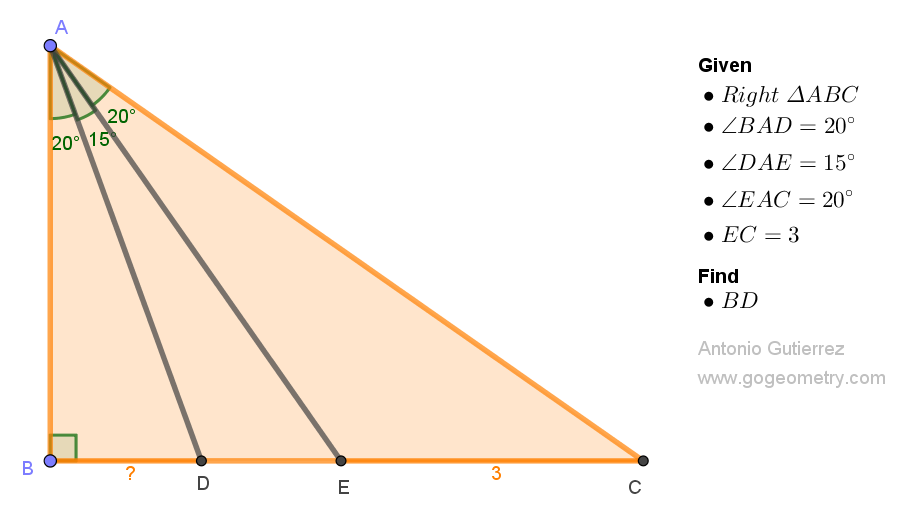
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Let AD & AE extended meet circle ABC (with diameter AC) at P & Q respectively.
ReplyDeleteDraw DM perpendicular to BP, M on BP
BP = CQ (both subtend 20 degrees on the circumference) = y, say
< ACB = < DBP = < DPB = 35 and so,
Triangle BDP is isosceles and hence BM = y/2
Triangles BDM & CEQ are similar (90,35,55) and so
BD/BM = CE/CQ
Therefore BD/(y/2) = 3/y which yields
BD = 3/2
Sumith Peiris
Moratuwa
Sri Lanka
Hi this ready...?
DeleteTrigonometry Solution
ReplyDeleteLet tan35 = t
BD = c.tan20 = c/tan70 = c./(tan(2X35) =c.(1-t^2)/2t........(1)
BE = c.tan35 = ct.......(2)
BC = c.tan55 = c/tan35 = c/t .......(3)
(3) - (2); CE = BC - BE = c.(1/t - t) from (2) & (3)
So c.(1-t^2)/t = 3......(4)
From (1) & (4) BD = 3/2
Sumith Peiris
Moratuwa
Sri Lanka
The trigonometric solution is beautiful because it is simple. The geometric solution is beautiful because it makes ingenious auxiliary constructions.
ReplyDeleteThank you
Delete2nd Geometry Solution - much simpler
ReplyDeleteLet FA be perpendicular to AC, F on CB extended
Let BD = x
Now FD = DA = DC so DE = a - x - 3 and FB = a - 2x
FB = BE = a - 2x = BD + DE = x + (a - 3 - x) = a - 3
Hence 2x = 3 and x = 3/2
Sumith Peiris
Moratuwa
Sri Lanka
Nice solution by creating the right triangle FAC.
ReplyDeleteNotice that AD=CD and, if ADCF is a rhombus, F is the circumcenter of triangle AEC, <FCE=<ADB, FC||=AD, G, projection of F onto CB is midpoint of EC, while triangles CFG and DAB are congruent, so CG=BD, done.
ReplyDeleteLet's assume that BD=x, DE=y, ADC is isosceles, so AD=DC=y+3
ReplyDeleteABE & ABC are similar by angles, so AB/x+y = x+y+3/AB so AB^2=(x+y)(x+y+3) ----1
In ABD, AB^2=(y+3)^2_x^2 -------2
From 1&2: (y+3)^2_x^2=(x+y)(x+y+3)
(y+3-x)(y+3+x)=(x+y)(x+y+3)
y+3-x=x+y
3-x=x
x=3/2