Geometry Problem 1548. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Get the full picture! Click below to uncover the details.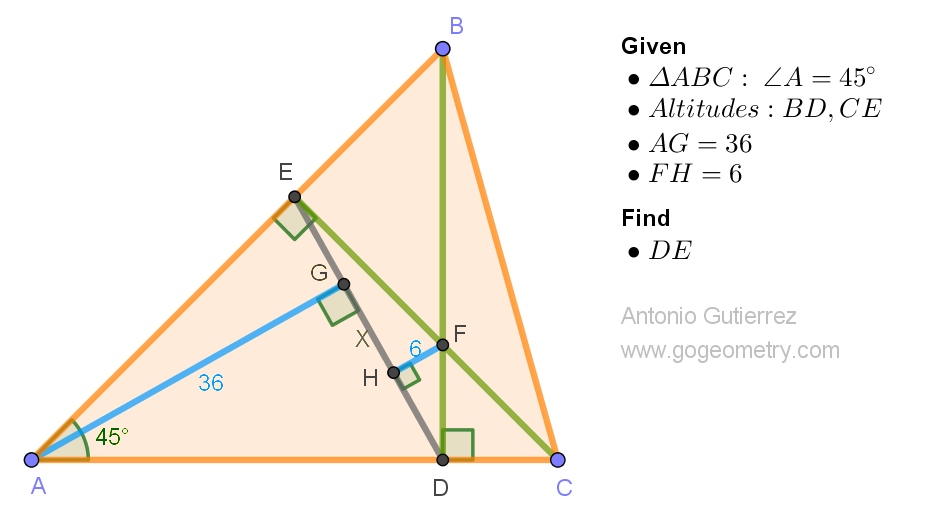
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Let BF = p so that BE = EF = p/V2
ReplyDeleteLet CF = q so that CD = q/V2
Triangles AGE & BCD are similar, hence
36/AE = BD/a so 36/(b/V2) = c/V2/(a) from which
bc = 72a..............(1)
Triangles EFH & BCD are similar. hence
6V2/p = q/V2/a so
pq = 12a.......(2)
Triangles AED & ABC are similar, hence
DE = a/V2.......(3)
Now apply Ptolemy's Theorem to cyclic quadrilateral BCDE
a.DE + (p/V2)(q/V2) = (b/V2).(c/V2) and so
a^2/V2 + pq/2 = bc/2 from which
a^2/V2 + 6a = 36a where we have substituted from (1) & (2)
Therefore from (3) DE = a/V2 = 30
Sumith Peiris
Moratuwa
Sri Lanka
Much simpler solution
DeleteDraw EPQ // BD, P on AG & Q on AC
BCDE is concyclic hence < AEG = C and < EAP = 90 - C = < CBD = < DEC
Consider Triangles AEP & CED
*AE = CE
*< EAP = < DEC = 90 - C
*< AEP = < < DCE = 45
So Triangles AEP & CED are congruent ASA
Hence AP = DE ......(1) and
EP = DC = FD since Tr. CDF is right isosceles
So Triangles EPG & DFH are congruent ASA
Hence PG = FH = 6 .....(2)
From (1) & (2), DE = AP = AG - PG = 36 - 6
DE = 30
Sumith Peiris
Moratuwa
Sri Lanka
This comment has been removed by the author.
ReplyDeleteConstruct the parallelogram DFEK, K is on AG an it is the orthocenter of tr. ADE, thus AK=AG-GK=AG-HF=30, but if <A=45, DE=AK, done.
ReplyDeletehow did you get DE=AK at angle A=45
Deleteproperty of angle of 45 degs!
Delete