Geometry Problem 1544. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Get the full picture! Click below to uncover the details.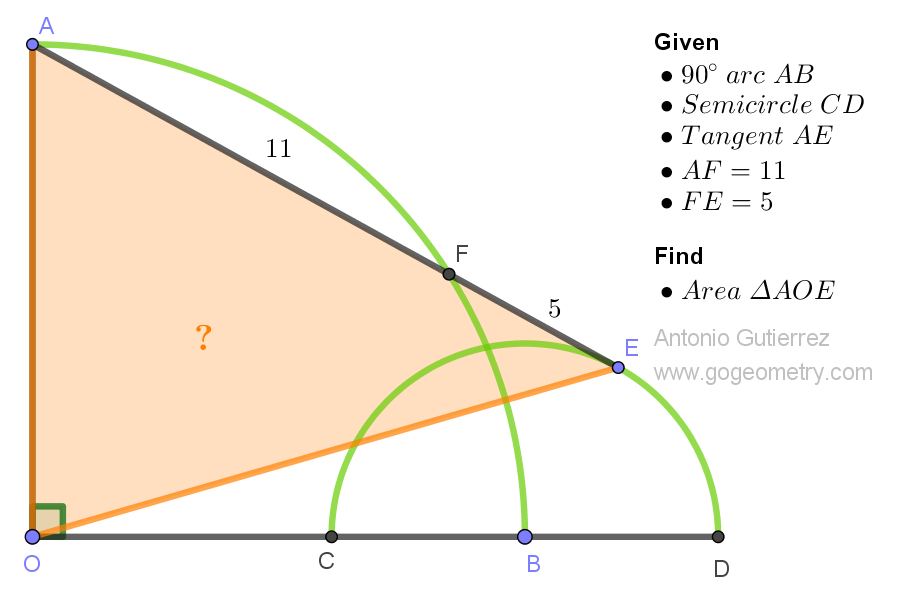
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Draw a perpendicular AU from A to OE, U on OE. Let BF cut OE at V.
ReplyDeleteLet OA = OF = OB = a and OU = p.
AOBE is concylic and AO = OB hence OE bisects < AEB (=90).
So Triangles FEV, BEV & FREB are all right isosceles.
< OFA = < OAF = < EBD so Triangles OFE & OBE are congruent ASA.
Now FV = 5 / V2 and AU = UE = 16/V2 = 8V2.
UV = 8V2 - 5/V2 = 11/V2
Now use Pythagoras on Triangles AOU & AEU.
a^2 = p^2 + 128 ...............(1)
a^2 = (p+11/V2)^2 + 25/2.......(2)
(2) - (1); 11V2p + 121/2 = 231/2 so p = 5/V2
OE = (5 + 11 + 5)/V2 = 21/V2
S(AOE ) = (1/2) AU. OE = (1/2). (8V2).(21/V2) = 84
Sumith Peiris
Moratuwa
Sri Lanka
84
ReplyDeleteSince AE is tangent to circle with Center B, Angle AEB = 90 deg,
ReplyDeleteAnd Angle AOB = 90 deg too, hence Quadrilateral AOBE is cyclic.
Angle AEO = Angle ABO = 45 deg.
Draw OH perpendicular AE. We get Triangle OHE as right isosceles triangle. (OH=HE)
Also H is midpoint of chord of AF, hence AH=HF=11/2
And OH = HE = HF + EF = 11/2 + 5 =21/2
Area of Triangle AOE = (1/2)OH.AE = (1/2)*(21/2)*16=84 square units.
Beautiful simple solution Pradyumna
DeleteThank you Sumith !!
Delete