Geometry Problem 1526. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.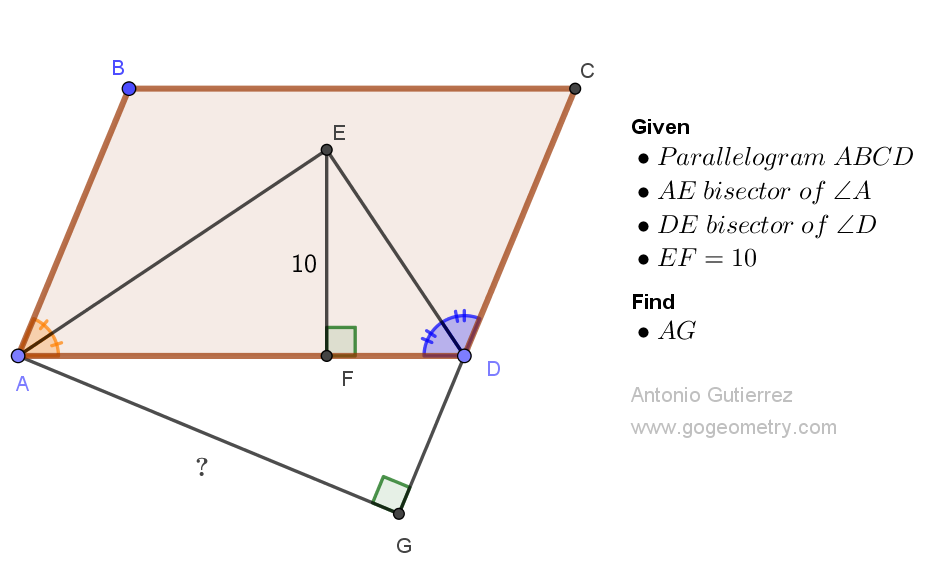
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
AG = 20
ReplyDeletehttps://photos.app.goo.gl/csBRn4k2btFAxqn86
Deletehttps://photos.app.goo.gl/GwyH5jPsyhtGKUD69
ReplyDeleteDefine point I as midpoint of AD and N is the projection of D over AB
Note that AED is the right triangle => IE=IA=ID
Since I is the incenter of triangle AED
So central angle ^(EID)= 2.^(EAD)= 2u=^(NAD)
Triangle IFE similar to AND ( case AA)
So ND/EF=AD/IE= 2
ND=AG=2.EF=20
This comment has been removed by the author.
ReplyDeleteLet AB, DE extended meet at U. Drop a perpendicular UP to AD, P on AD.
ReplyDeleteTriangles AEU & AED are congruent ASA & so AU = AD
E is midpoint of DU hence from the midpoint theorem UP = 2 X 10 = 20
Now Triangles APU & ADG are congruent ASA (since AU = AD)
So AG = UP = 20
Sumith Peiris
Moratuwa
Sri Lanka
Let K, L be projections of E onto AB, CD, then E being onto the angles bisectors, KE=EF=EL=10, but K-E-L are collinear...
ReplyDeleteAnswer is 20
ReplyDelete