Geometry Problem 1524. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.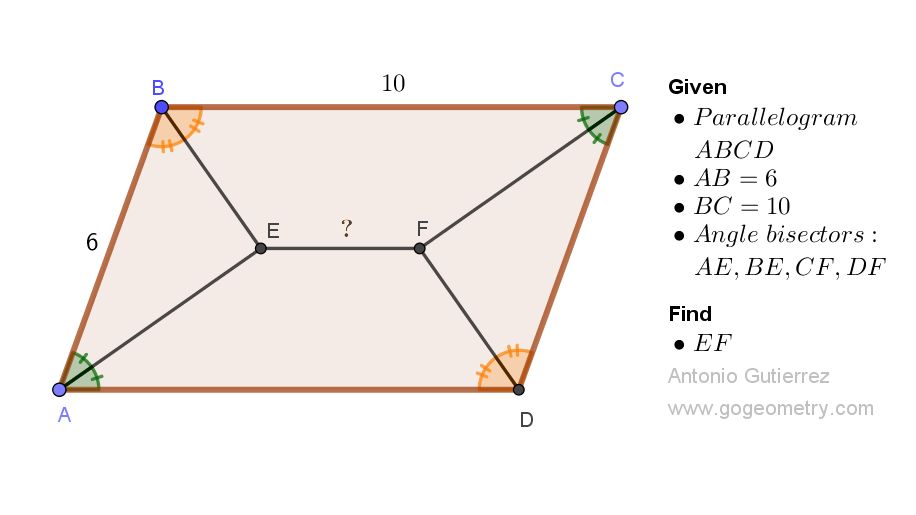
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Let AE,DF extended meet at X and let BE,CF extended meet at Y.
ReplyDeleteLet BE = DF = p and AE = FC = q. Let FY = u and EY = v
< ABC & < BAD are supplementary and so < ABE & < BAE are complementary
Hence EX FY is a Rectangle
From similar triangles ABE & BYC,
(p+v)/p = (q+u)/q = 10/6
So u = 2q/3 and v = 2p/3
Applying Pythagoras to Triangles ABE & EYF,
EF^2 = u^2 + v^2 = (2/3)^2. (p^2 + q^2) = (2/3)^2. (6^2) = (4/9)*36 = 16
Therefore EF = 4
Sumith Peiris
Moratuwa
Sri Lanka
Extend DF to P => BP=10 - 6 = EF
ReplyDeleteHow is BP = EF?
DeleteOn what basis is BP = EF?
Delete( BE = PF, & BE // PF ) => BPFE parallelogram
DeleteDear Peter - could you explain how you concluded that points M,E,F,N are collinear which is essential for your proof to be valid?
ReplyDeleteRegards
Sumith
Since M and N are midpoints of AB and CD => MN//BC
ReplyDeleteME//BC and NF //BC => M,E, F ,N are collinear
Thanks
Delete. o 1 continue line segment df to point z on bc
ReplyDeleteEF=10-(2×3)=4
ReplyDelete