Geometry Problem 1517. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.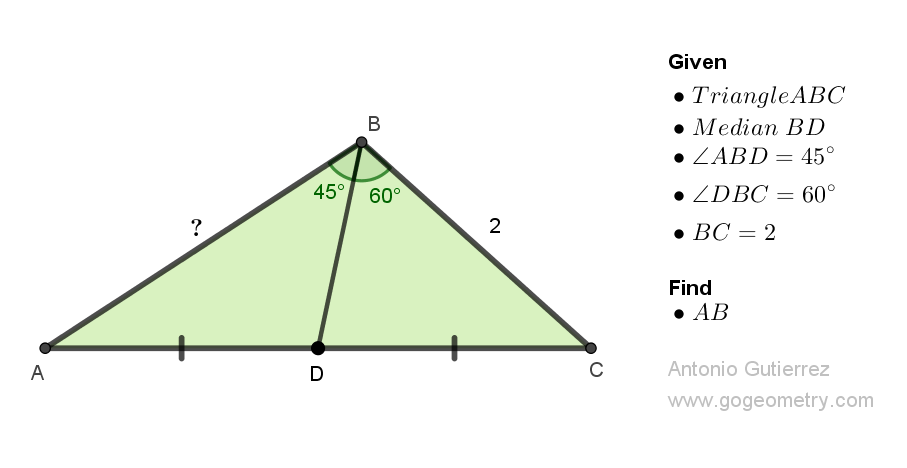
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
V6 (sqrt of 6)
ReplyDeletehttps://photos.app.goo.gl/CkcFLDMpaKUyBK3a9
DeleteDrop perpendiculars DP and DQ from D to AB and from D to BC, P on AB and Q on BC respectively.
ReplyDeleteSince AD = DC, S(ABD) = S(BDC)
So AB.DP/2 = BC.DQ/2
Hence (c/2)d/(sqrt2) = (1/2).2. (sqrt3./2)d
Simplifying c = sqrt 6
Sumith Peiris
Moratuwa
Sri Lanka
Construct parallelogram BAEC.
ReplyDeleteDrop perpendicular AH, from A to BE.
AEH is a 30-60-90 triangle, and ABH is a 45-45-90 triangle.
BC=AE=2, AH=sqrt 3, AB=sqrt 6.
AB/AD = sin D / sin 45.
ReplyDeleteDC/BC = sin 60 / sin 45.
Multiply side by side
AB/BC = sqrt 3 / sqrt 2 => AB = sqrt 6.
sqrt(6)
ReplyDelete