Geometry Problem 1512. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.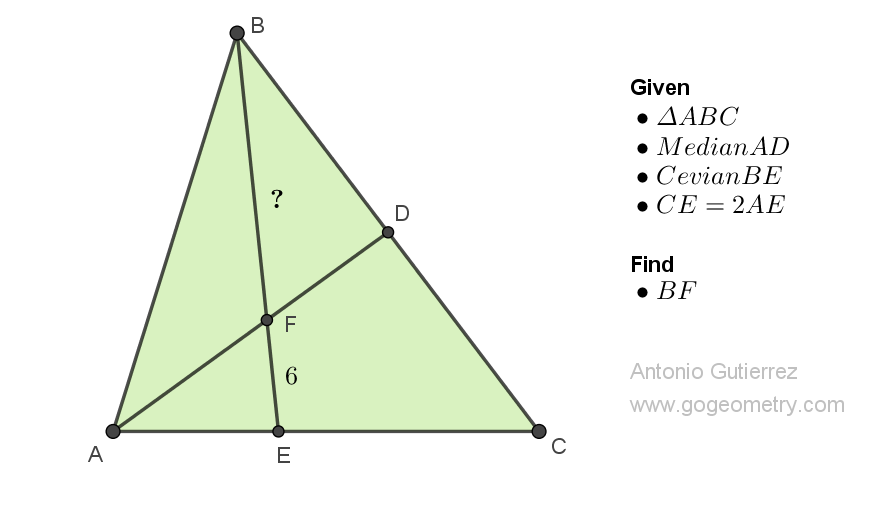
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
https://photos.app.goo.gl/Rr1mPzhRSN29rhfb6
ReplyDeleteLet CF meet AB at G
Apply Ceva theorem for concurrent point F we have (EA/EC) x(DC/DB) x( GB/GA)= 1
Replace DC/DB= 1 and EA/EC=½ we get GB/GA= 2
Apply Van Aubel theorem we have FB/FE= GB/GA + DB/DC = 2+1= 3
So BF= 3GA= 18
https://photos.app.goo.gl/cDwW2cJUjC13tptQ9
ReplyDeleteIf G is the mid point of BE, from the mid point theorem,
ReplyDeleteGD = CE/2 = AE
Then Tr.s AEF & DFG are congruent ASA
So GF = EF = 6 and so GE = 6 + 6 = 12
Hence BF = BG + GF = GE + GF = 12 + 6 = 18
Sumith Peiris
Moratuwa
Sri Lanka
From Rimitti / Wahran / Algeria
ReplyDeleteApply Menelau's theorem to triangle EBC and secant AFD :
(BD/DC)*(CA/AE)*(EF/FB) = 1 with CA= 3AE and BD=DC ---> 3*EF/FB = 1---> FB =18