Geometry Problem 1504. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.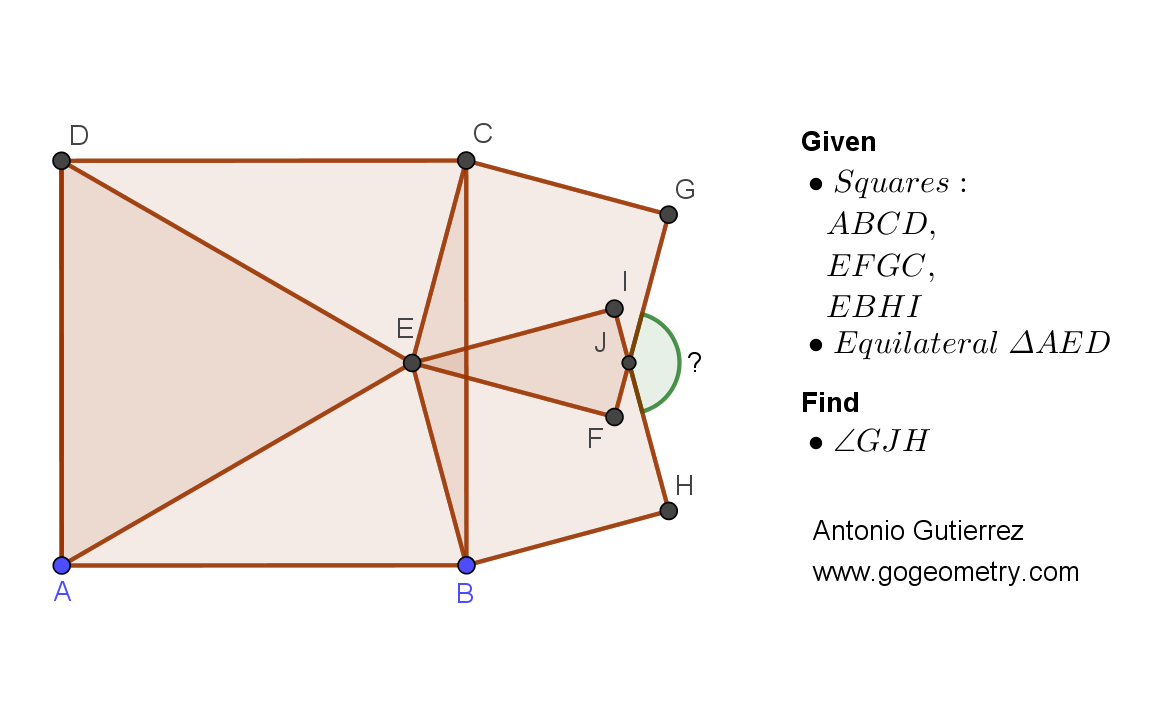
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Tr. CEB is isoceles with angles 15,15,150
ReplyDeleteTr.s CEI & BEF are congruent SAS
If < CEI = < BEF = p then considering the angles in Tr. BEC, 15+15+p + p + 90-p = 180
So p = 60 and < IEF = 30 and so < GJH = 150
Sumith Peiris
Moratuwa
Sri Lanka
2 interesting results
Delete1 - FC is perpendicular to AC
2 - Tr. BIF and Tr. JFH have angles 15,30 and 135
A simpler solution
ReplyDeleteSince < BEC = 150 and < FEC = 90, < BEF = 60 so < EFI = 30
Hence considering cyclic quadrilateral EIJF, < GJH = 150
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/poMiXSFHd2rRzTxS6
ReplyDeleteConstruct equilateral triangle CBP as shown
Note that triangle CBP is the translation of triangle DAE with EP=DC and DE=CP
Since EP is an angle bisector of ∠(CPB) > ∠(CPE)=30
Since EP=CP -> CEP is isoceles - > ∠(CEP)=∠(ECP)= 75 and ∠(ECB)= 15
So ∠(CEB)= ∠(GJH)= 150