Sunday, December 28, 2025

Geometry Problem 1611: Angle Calculation in Triangle ABC

Challenging Geometry Problem 1611. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.

Gain comprehensive insights! Click below to reveal the complete details.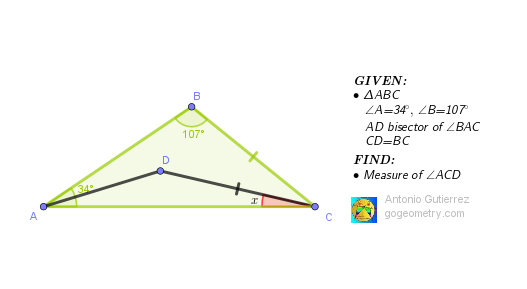

Illustration of Geometry Problem 1611

Click for additional details.

Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.



Posted by Antonio Gutierrez at 5:07 PM

1 comment:

  1. Sumith PeirisDecember 29, 2025 at 7:08 AM

    Thanks for the hint Antonio

    The perpendicular from C to AD extended meets at E. CE extended meets AB extended at F

    < FBC = 73 = < ACF = < AFC

    So FC = CB = CD = DF, hence Triangle CDF is equilateral

    Hence < BCD = 60 - 34 = 26 and
    x = 39 - 26 = 13

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete

Share your solution or comment below! Your input is valuable and may be shared with the community.

Subscribe to: Post Comments (Atom)