Challenging Geometry Problem 1606. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.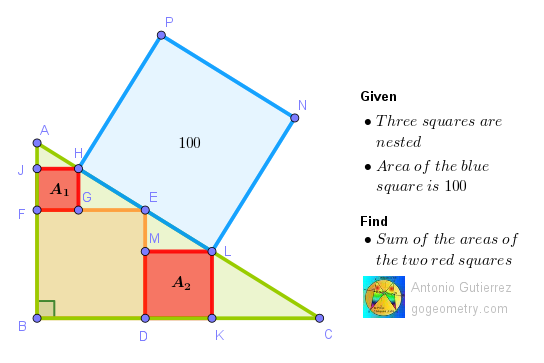
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Let square BDEF be of side u, square FGHJ of side v and DKLM of side w
ReplyDeleteTriangles HGE & EML are similar so GE/GH = ML / ME
Hence (u-v)/v = w/(w-u), which yields u = v + w upon simplifying the Algebra.
So ME = u-w = v = HG
Similarly ML = w = u - v = GE and hence
Triangles HGE & EML are congruent SAS
So HE = EL = 5
Therefore A1 + A2 = v^2 + w^2 = HE^2 = 25
Sumith Peiris
Moratuwa
Sri Lanka