Challenging Geometry Problem 1605. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.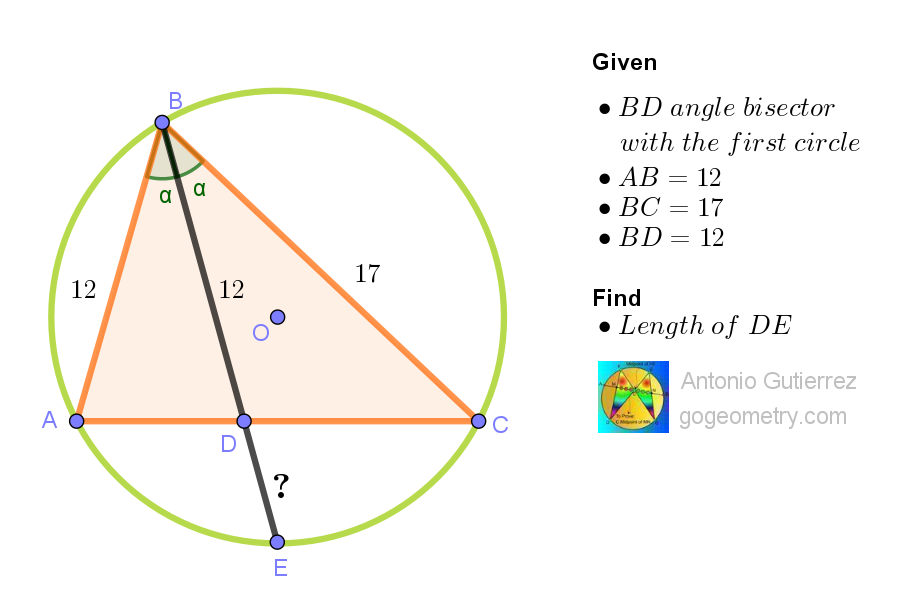
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
We see that Triangles ABD & CBE are similar (having angles @ and 90 - @/2)
ReplyDeleteSince Triangle ABD is isosceles, hence so is Triangle CBE
Therefore BE = BC and
DE = 17 - 12 = 5
Sumith Peiris
Moratuwa
Sri Lanka
excellent solution
DeleteFurther,
Delete1) Triangle CDE is also isosceles
2) AE = EC = CD = V85
3) AD = 60/V85
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/hVn8UATWfUn5dfLC9
ReplyDeleteLet AE=EC=z and BE=y
In triangle ABE we have z^2= 12^2+y^2- 2.12.ỵ cos(alpha)..... (1)
In triangle BEC we have z^2= 17^2+y^2-2.17.ỵcos(alpha)...... (2)
Multiple (1) by 17 ….. (3)
Multiple (2) by 12……(4)
Subtract line(3) to line (4)
Simplify the result and we get z^2=y^2-204
Triangle ABE similar to DAE ( case AA)
So AE^2=z^2= DE . EB= y( y-12)= y^2-204
So y= 17 and DE=5
1. BD is the angle bisector.
ReplyDeleteAD: DC = 12:17.
2. ΔAEC is an isosceles triangle.
3. Triangles AEC and BAE are similar.
4. By the power of a point theorem,
DA × DC = DB × DE.
5. By Ptolemy's theorem,
AB × EC + BC × AE = BE × AC.
From these equations, we can conclude that DE = 5.
Another solution:
ReplyDeleteThe area of triangle ABC is
S = (1/2) × 12 × 17 × sin(2α) = (1/2) × 12 × 12 × sin(α) + (1/2) × 12 × 17 × sin(α).
Therefore, cos α = 29/34.
AE = EC, so by the law of cosines, BE = x.
12² + x² - 2 × 12 × x × cos α = 17² + x² - 2 × 17 × x × cos α
Solving this equation yields x = 17.
Therefore, DE = 5.
AB.BC=BD.BE, so BE=12×17/12=17.So, DE=17-12=5
ReplyDelete