Challenging Geometry Puzzle: Problem 1598. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.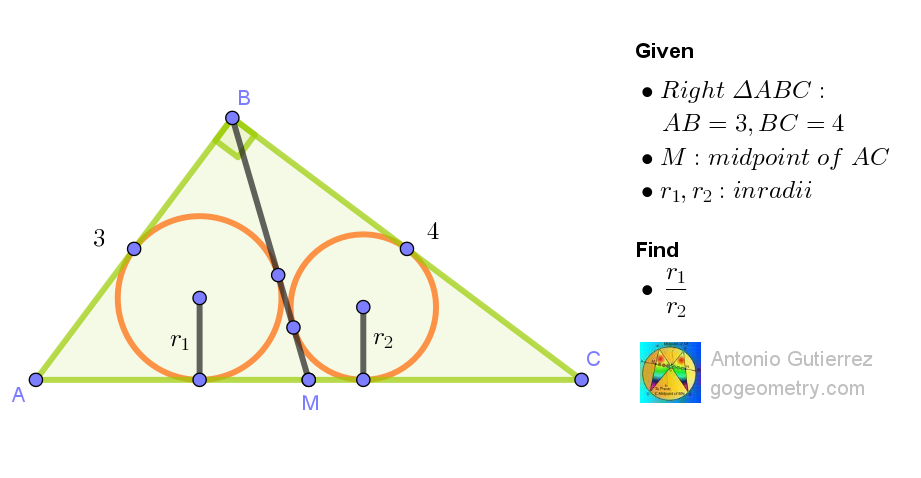
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
From the median theorem AB^2+BC^2=2(BM^2+MC^2)
ReplyDelete9+16=2(BM^2+25/4)
From this, BM=5/2
Also, from the area of △ABM = area of △CBM
r1(AB+BM+MC)/2=r2(CB+BM+MC)
r1(3+5/2+5/2)=r2(4+5/2+5/2)
8r1=9r2
Therefore, r1/r2=9/8
We have S(ABM)=S(BMC)= p1.r1= p2.r2 ( same height and equal bases)
ReplyDeletewhere p1 and p2 are half perimeter of triangles ABM and BMC
we have AC=5 and AM=MC=MB= 2.5
and 2p1= 8, and 2p2=9
r1/r2= p2/p1= 9/8
S(ABM) = S(CBM) = (1/2) X (3 X 4 / 2 ) = 3
ReplyDeleter1 = S(ABM) / s1 = 3 / (8/2) = 3/4 and
r2 = S(CBM) / s2 = 3 / (9 / 2) = 2/3
Hence r1 / r2 = (3/4) / (2/3) = 9 / 8
Sumith Peiris
Moratuwa
Sri Lanka
Let O1 and O2 be the centers of the incircles with radii r1 and r2, respectively. Let P and Q be the midpoints of sides AB and BC, respectively. Since ABC is a right triangle with legs 3 and 4, AC must have length 5, which means AM = BM = CM = 5/2. It follows that AMB and CMB are isosceles triangles so that the bisector of the angle between their congruent sides is also an altitude. Thus, MPBQ is a rectangle with sides 2 and 3/2. As a result, triangles AMB and CMB have equal area. Using the fact that the area of a triangle is the product of half its perimeter and the length of its inradius, (3 + 5/2 + 5/2)/2 * r1 = (4 + 5/2 + 5/2)/2 * r2, so that r1/r2 = 9/8.
ReplyDeleteABC is 3,4,5 triangle
ReplyDeleteABM & BCM are is isosceles triangles
AM = BM = CM = 2.5
height of: ABM = 2, & BCM = 1.5
r1 = AB/4 = 3/4, r2 = BC/6 = 4/6
r1/r2 9/8