Challenging Geometry Puzzle: Problem 1563. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.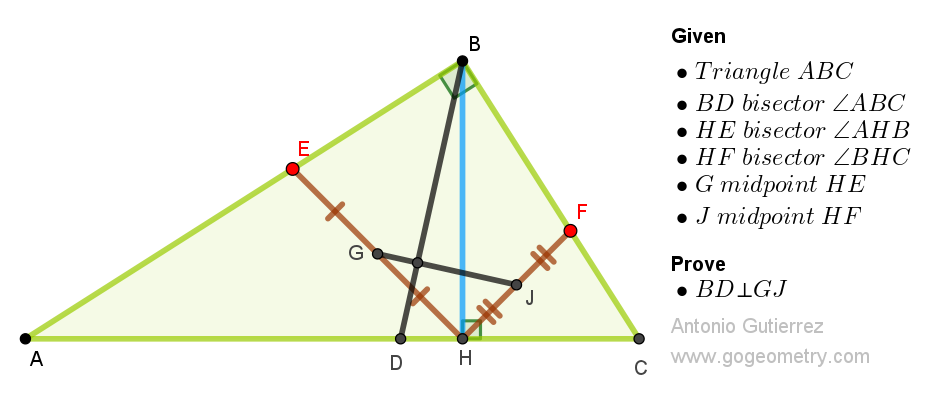
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Draw EF intersects BD at M
ReplyDelete<EHF=<EBF=90° thus B, E, H, F concyclic
<BEF=<BHF=45°=<EBD thus <BME=90°→ BD┴EF (1)
J, G midpoints of HE and HF hence GJ//EF (2)
From (1),(2) have BD┴GJ
Let BD and EF cut at K
ReplyDeleteBEHF is a circle with EF as diameter, hence < BEF = < BHF = 45
Hence BEK, BFK & BEF are all right isosceles triangles and EF is thus perpendicular to BD
Since EF // GJ, it follows that GJ is also perpendicular to BD
Sumith Peiris
Moratuwa
Sri Lanka