Challenging Geometry Puzzle: Problem 1561. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.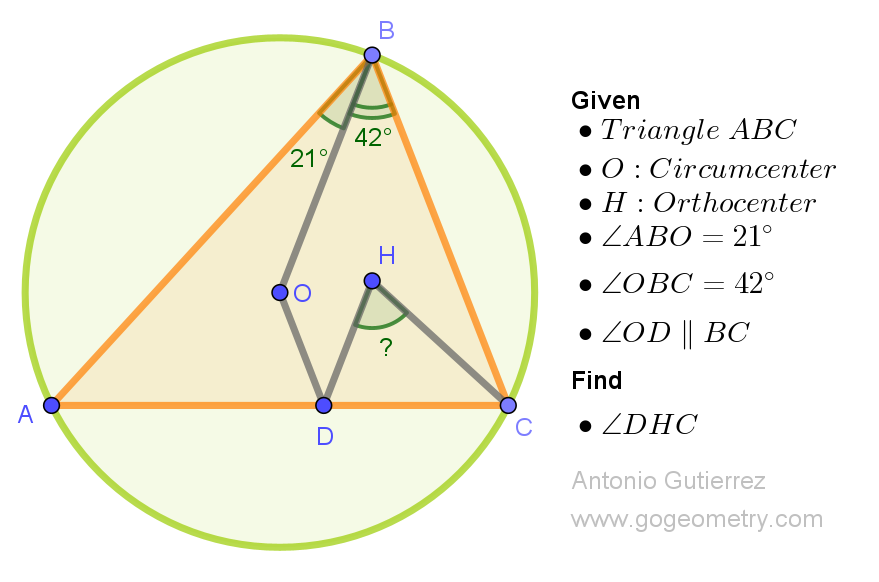
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
See diagram here.
ReplyDeleteExtend BO to intersect AC in E, OD to intersect (O) in F and BH to intersect (O) in G.
We have :
- ΔAOB and ΔBOC isosceles in O ⇒ ∠OAB = ∠ABO = 21° and ∠BCO = ∠CBO = 42°
- ΔAOC isosceles in O and ∠AOC = 2. ∠ABC = 126° ⇒ ∠OAC =∠OCA = (180-∠ABC)/2 = 27°
- ∠BAC = ∠OAB + ∠OAC = 48°
- CH being the altitude from C ⇒ ∠HCA = 90°- ∠BAC = 42°
- In ΔBCE, ∠BCE = ∠BCA = ∠BCO + ∠OAC = 69° and ∠BEC = 180°- ∠BCE - ∠CBO = 69° so ΔBCE is isosceles in B and therefore H, being the altitude from B, also lies on the bisector of ∠CBE
- Hence ∠OBG = ∠OBH = ∠EBH = 21°
- Also, since OD is // to BC, ∠ODA = ∠BCA = 69° = ∠OCA + ∠COD, therefore ∠COD = 42° and ∠BOD = 2.∠BAC + ∠COD = 138°
By construction of F and G, ΔBOF and ΔBOG are both isosceles in O.
In ΔBOF, ∠OBF = (180-∠BOF )/2 = (180-∠BOD )/2 = 21° = ∠OBG = ∠OBH = means that H lies on BF, so that BH and OD actually intersect on (O) in F = G which are one and the same.
Now :
- In ΔGCH, ∠CFH = ∠CFB = ∠CAB = 48° and ∠CHF = 90° - ∠HCA = 48° so ΔGCH is isosceles in C and CH = CF
- In ΔDCF, ∠CDF = ∠ODA = 69° and ∠CFD = 180° - ∠CDF - ∠DCF = 111 - ∠ABF = 69° so that ΔDCF is isosceles in C and CD = CF
So: CH = CD, ΔDCH is isosceles in C and ∠DHC = (180-∠HCD)/2 = (180-∠HCA )/2 = 69°
Let BO extended meet AC at X, BH extended meet AC at U & OD extended at Y, Z be on BC extended, AH extended meet BC at V and let CH extended meet AB at W
ReplyDelete< VAB = 90 - 21 - 42 = 27 and < OAB = OBA = 21 & < OAV = 27 - 21 = 6
< AOC = 2 X < ABC = 126 & so < OCA = OAC = 27 & <VAC = 27 - 6 = 21
Now < BCO = < CBO = 42 & < BCW = 90 - 21 - 42 = 27 & so < OCW = 15
Hence < XOY = < CBO = 42 = < BCO = < COY & OY bisects < XOC
Also < CBU = 90 - 69 = 21 & so BY bisects < CBX
It follows that Y is the excentre of Triangle BOC & so YC bisects < OCZ
So < OCY = 69 & < DCY = 69 - 27 = 42 & since < CDY = < DCB = 69, < DYC = 69
But Triangles HCU & YCU are congruent SAS & So HC = YC = DC
Hence C is the Circumcentre pf Triangle HDY and so < DHY = 1/2 of < DCY = 21
Therefore < CHC = 21 + 48 = 69
Sumith Peiris
Moratuwa
Sri Lanka
It seems that whatever "angle hunting we do" the key is to consider the circumscribed circle. You used even more. It seems that it is enough to draw only the circumscribed circle of triangle ABC, as in Greg's post. I will try another way using a property of the points O and H and the construction of the symmetry of H with respect to the side BC (which actually belongs to the circumscribed circle as well)
ReplyDelete