Challenging Geometry Puzzle: Problem 1560. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.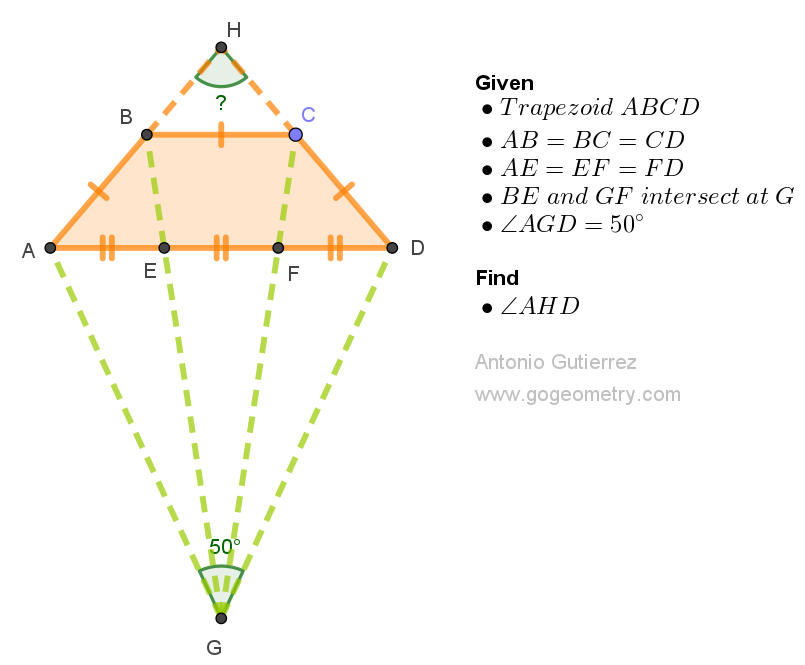
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
https://ibb.co/YjFM8Gg
ReplyDeleteImage of the solution.
ADH is isosceles and AGD is isosceles so AHDG is a deltoid. Let HG meets BC at point M, HG meets AD at point L. < HLD is a right angle.
Let GD and BC extended meets at point N.
< BNG = 65
Let AE = 2a, AB = 2k
Because of LF = a and FD = 2a then MC = k and CN = 2k, so CDN is isosceles.
< CDN = < CND = 65
Then < HDA = 180 - (< CDN + < ADG) = 50 and GHD = 40
< AHD = < LHD + < AHL
< AHD = 80
Let CB, GA extended meet at P
ReplyDeleteSince PC//AF and AE = EF, it follows that PB = BC = BA
Hence < PAC = 90 and < CAD = 90 - 65 = 25
Since ABCD is an isosceles trapezoid it is also concyclic
Hence < CAB = < CAD = 25
So < BAD = 50 = < HBC since BC//AD
Similarly < BCH = 50
Therefore < AHC = 180 - 50 - 50 = 80
Sumith Peiris
Moratuwa
Sri Lanka
To determine the measure of angle ( \angle AHD ) in the given trapezoid ( ABCD ), let’s break down the problem step-by-step:
ReplyDeleteIdentify Key Points and Relationships:
Trapezoid ( ABCD ) with ( AB = BC = CD ).
Points ( E ) and ( F ) on ( AD ) such that ( AE = EF = FD ).
Extensions of ( BE ) and ( CF ) intersect at ( G ).
Extensions of ( AB ) and ( DC ) intersect at ( H ).
Given ( \angle AGD = 50^\circ ).
Use Geometric Properties:
Since ( AB = BC = CD ), ( ABCD ) is an isosceles trapezoid.
( AE = EF = FD ) divides ( AD ) into three equal segments.
Apply Angle Properties:
( \angle AGD ) is given as ( 50^\circ ).
Since ( G ) is the intersection of ( BE ) and ( CF ), and ( H ) is the intersection of ( AB ) and ( DC ), use the properties of intersecting lines and angles.
Calculate ( \angle AHD ):
By the properties of intersecting lines and the given angle, ( \angle AHD ) can be determined using supplementary angles and the sum of angles in a triangle.
Given ( \angle AGD = 50^\circ ), and knowing the geometric properties, ( \angle AHD ) can be calculated as ( 180^\circ - 50^\circ = 130^\circ ).
Thus, the measure of ( \angle AHD ) is ( 130^\circ ).