Saturday, September 23, 2023

Geometry Problem 1554: Finding the Length of Side AB in Triangle ABC

Challenging Geometry Puzzle: Problem 1554. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.

Gain comprehensive insights! Click below to reveal the complete details.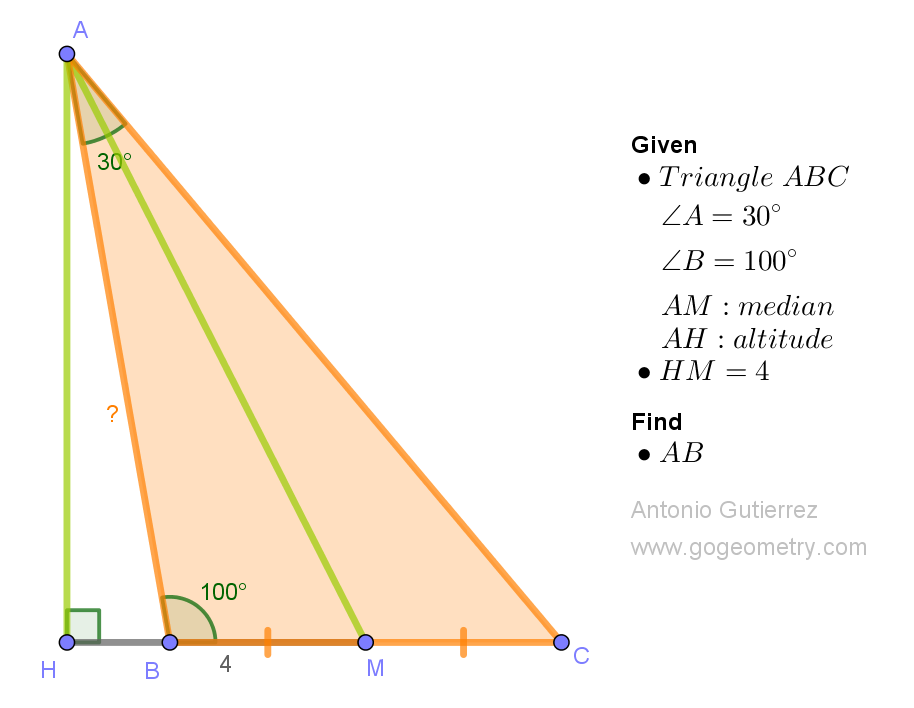

Illustration of Problem 1553: Geometry Problem 1554: Finding the Length of Side AB in Triangle ABC

Click for additional details.

Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.

Posted by Antonio Gutierrez at 4:41 PM
Labels: , , , , ,

6 comments:

  1. Sumith PeirisSeptember 24, 2023 at 12:40 AM

    Extend BH to D and E such that < ADH = 80 and < AEH = 50.
    Extend BC to F such that < AFH = 40

    Now Triangle EAF is Right Angled with B as centre
    Hence AD = AB = BF = BE = c
    So CF = c - a
    BD = 2 X (4 - a/2) = 8 - a and DE = a (since Triangles ADE & ABC are congruent ASA)
    Hence c = BE = BD + DE = (8 - a) + a = 8

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete
  2. Sumith PeirisSeptember 27, 2023 at 12:46 AM

    Slightly modified solution

    Draw a Circle AEF with Centre B and Radius BA so that EHBMCF is a Diameter. Mark D on HE such that DH = BH = 4 - a/2 and AD = AB = c

    Triangles ABD & ADE are both isosceles and Triangles ADH and ABC are congruent ASA
    So DE = BC = a and BD = c - a
    But BD = BH X 2 = (4 - a/2) X 2 = 8 - a
    Hence BD = c - a = 8 - a and c = 8 = AB

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete
  3. AnonymousJanuary 23, 2024 at 4:20 AM

    Amazing..... Great Sri lankan son




    ReplyDelete
  4. AnonymousApril 25, 2024 at 8:10 AM

    Let the bisector of angle ABC intersect AC at D.
    Since <DCB = <DBC= 50, DBC will be an isosceles triangle.
    Draw DM which will be parallel to AH.
    From similarity, CM/MH = CD/DA.
    And from angle bisector theorem BC/BA=CD/DA
    Hence, CM/MH = BC/BA
    Since BC = 2 CM, BA = 2 MH = 2*4 = 8.

    ReplyDelete
  5. AnonymousJuly 21, 2024 at 10:32 AM

    Take a point D symmetric to B relative to AH. Then we immediately see that DH = HB and AD = AB (1).
    Also, angle <ABH = 180º - 100º = 80º, and angle <ADH = 80º. In triangle ABC angle <ACB = 180º - 100º - 30º = 50º. So in triangle ADC, <DCA = <BCA = 50º and angle <DAC = 180º - 80º - 50º = 50º, and we conclude that ADC is and isosceles triangle with AD = DC, and by (1) AB = DC.
    But DC = DH + HB + BM + MC, with DH = HB, MC = BM, and HB + BM = 4 (by hypothesis), so,
    DC = HB + HB + BM + BM = 2*(HB + BM) = 2*HM = 2*4 = 8; as AB = DC, then finally
    AB = 8.

    Joaquim Maia
    Rio de Janeiro
    Brazil

    ReplyDelete
  6. Stan FULGEROctober 26, 2024 at 12:50 AM

    My solution at https://stanfulger.blogspot.com/2024/10/httpsgogeometryblogspotcom202309geometr.html

    ReplyDelete

Subscribe to: Post Comments (Atom)