Challenging Geometry Puzzle: Problem 1551. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.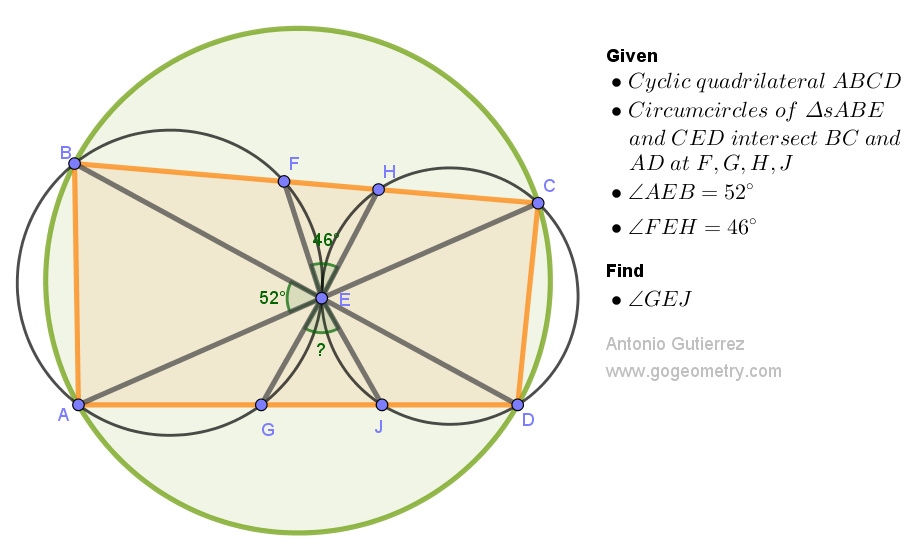
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
< FBE = < FAE = < CAD = < FGE = a (say)
ReplyDelete< JHE = < HEJ = < BDH = < BDA = b (say)
< FEB = < FAB = < FGB = u (say)
< HEC = < HJC = < HDC = v (say)
< ABG = < AFG = < AEG = t (say)
< JCD = < JHD = < JED = y (say)
a + b = 52.........(1) (Triangle BCE)
u + v + 52 + 46 = 180 (angles on Point E)
So u +v = 82 .......(2)
u + 2a + t = 180 - 52 = 128...(3) (Angles on Point G)
v + 2b + y = 180 - 52 = 128 ...(4) (Angles on Point J)
(3)+(4) ==> u + v + 2a + 2b + t +y = 256
So 82 + 104 + t + y = 256
t + y = 70
< GEJ = 180 - (a+t) - (b+y) = 180 - (a+b) - (t+y) = 180 - 52 - 70
< GEJ = 58
Sumith Peiris
Moratuwa
Sri Lanka
Because < BDC= < BAC;
ReplyDeleteSo, < HFE= < FHE
Same for <EGJ = EJG
So < FHE =90-46/2 = 67 degree
So < EDC = 67 degree
So < ECD =180 -52-67 = 61 degree
So < EJG =61 degree
So <GEJ = 2*(90-61)= 58 degree
Antonio - a new problem arises from this problem
ReplyDeleteProve that FHJG is a cyclic quadrilateral