Geometry Problem 1537. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Get the full picture! Click below to uncover the details.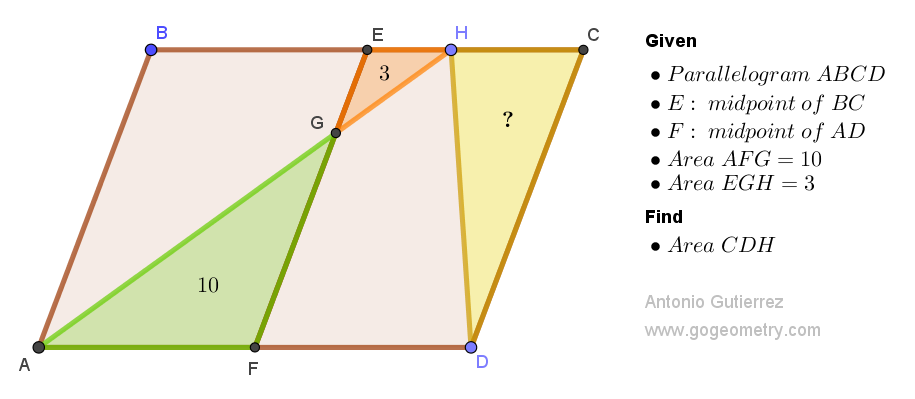
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Let S(CHD) = X, S(AEG) = Y. Let the height between AD & BC be h.
ReplyDeleteLet AF = a and EH = p
So S(AEF) = 10 + Y = ah/2 ......(1)
and S(AEH) = 3 +Y = ap/2 ........(2)
(1) - (2); X = (a-p).h/2 = 10 +Y - (3 + Y) = 7
Sumith Peiris
Moratuwa
Sri Lanka
https://photos.app.goo.gl/hsSdBqPvrrEzUCPTA
ReplyDeleteLet a= AF=EC
Let h= height of parallelogram ABCD
Let h1 and h2 are heights shown in the stretch
Let [XYZ]= area of triangle XYZ
Let u= EH/AF= h1/h2=u
We have h1= ụh/(1+u)
And h2= h/(1+u)
Calculate [AGF]=½.a .h2= ½. (ah)/(1+u)
Calculate [GEH]= ½. h1.EH= 1/2/ (au^2)/(1+u)
Calculate [HCD]=½(a-EH)(h)=1/2a.h.(1-u)
Verify that with any the value of u and h we always have [AGF]=[GEH]+[HCD]
So [HCD]= [AGF]-[GEH]= 10- 3= 7
Since FGE and AGH are straight lines, the ratio of AF and EH = 10 : 3, and because point E and F are the midpoints of AD and BC respectively AF : EH : HC = 10 : 3 : 7 and the ratio of the heights of triangles AFG, EGH and HCD is 10 : 3 : 13, the ratio of [AFG] and [AFEB] is 50 : 130, since the area of AFG is 10 the area of AFEB is 135/5= 66, because E and F are both the midpoints of AD and BC [AFEB]=[FDEC] so ratio of [FDEC] and [HCD] is 20 : 7 and the area of [FDEC] is 66 so the area of [HCD] is 7/20[FDEC] = 23.1
ReplyDelete