Geometry Problem 1533. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.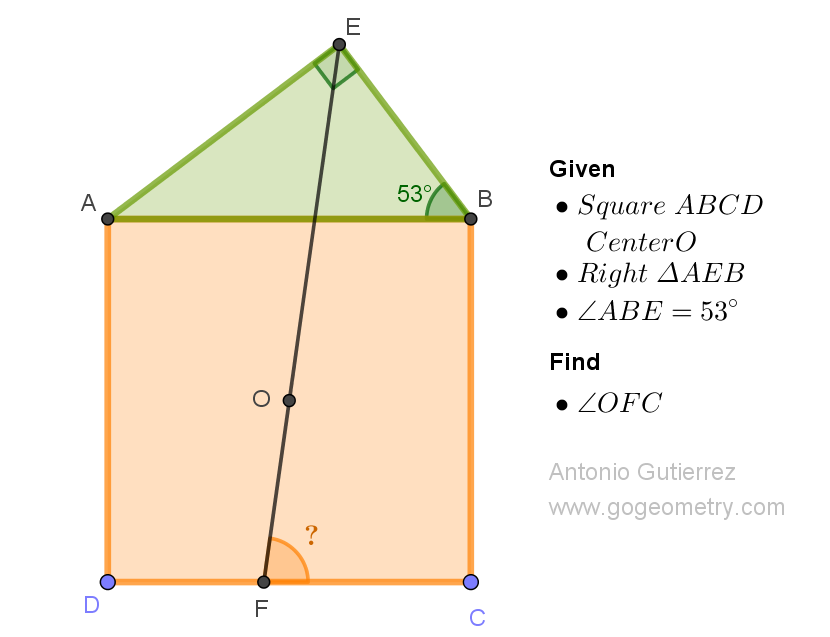
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Ang x = 82°
ReplyDeleteLet EF cut AB at P.
ReplyDeleteAOBE is a cyclic quadrilateral with AB as diameter.
So since AO=OB, OE bisects <AEB
So OFC = < BPE = 180 - 45 - 53 = 82.
Sumith Peiris
Moratuwa
Sri Lanka
Hi ! This problem is original, is simple , but you decide to display for solution if you think it is appropriate, Thanks
ReplyDeletehttps://photos.app.goo.gl/5dpTKYTQDr462XLL7
ReplyDeleteSame reasoning
ReplyDeleteLet AB ∩ EO = K
∠AOB = 90° (1)
∠AEB = 90° (2)
(1)(2)
⇒ AEBO = cyclic quadrilateral ØAB
⇒ ∠AOK = ∠ABE = 53° (3)
△OAB :
OA = OB
⇒ △OAB isosceles and rectangle at O
⇒ ∠BAO = ∠AOB = 45° (4)
△AKO
(3)(4)
⇒ ∠AKO = 180° - (45° + 53°)
= 82°
= ∠OFC, the dolution