Geometry Problem 1507. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.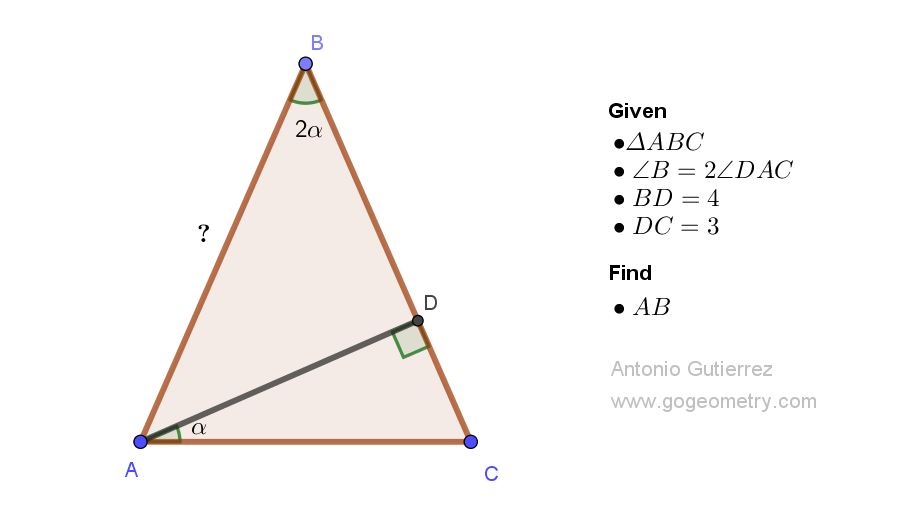
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
According to the Diagram <B = 2@.....................Case 1
ReplyDeleteAccording to the Data given <B = @...................Case 2
Case 1:-
Let BE bisect <B, E on AC
Hence ABDE is concyclic and BE is perpendicular to AC
So AB = BC = 3+4 = 7
Case 2:-
<CAD = <B = @
So AC is tangential to circle ABD at A
Hence AC = sqrt (3 X 7) = sqrt21 and so
AD = sqrt (21 - 9) = sqrt12
Therefore AB = sqrt(12 + 16) = sqrt 28 = 2.sqrt7
Sumith Peiris
Moratuwa
Sri Lanka
Thank you, Sumith, for your solutions and observation. To unify the idea, the graph has been modified to address Case 1.
DeleteTr ABC => isosceles => AB=7 (the sketch will come soon)
ReplyDeletehttps://photos.app.goo.gl/QSZMRAiAmrBdUsbQA
Deletehttps://photos.app.goo.gl/v4gnknaopkZNweet5
Delete=7
ReplyDeleteThank you Peter for your prompt solution
ReplyDelete1st solution: Let CE be the C- altitude, H - orthocenter; BEHD being cyclic, <CHD=<B=2@, or <ACH=@, AB=BC.
ReplyDelete2nd solution: Take F reflection of C about D, AC is tangent to the circle AFB and from p.o.p. AC^2=CF.BC= 6.7 ; by Pithagoras AD^2=AC^2-BD^2=42-9=33 and AB^2=AD^2+BD^2=33+16=49, AB=BC=7
We can use trigonometry to find the length of segment AD, then we'll use the Pythagorean Theorem on triangle ABD to find the length of AB.
ReplyDeleteSegment AD is adjacent to angle a. Segment DC, the measure of which we know, is opposite to that angle. So, we can use the tan trig ratio... tan(x) = 3/y. If you're confused as to where I'm going with this so far, stay tuned. Segment AD is opposite to angle 2a, and we know the measure of segment BD. We can once again use tan: tan(2x) = y/4.
We are now left with two equations:
tan(x) = 3/y
tan(2x) = y/4
If we apply the inverse of tan to both of them, then we are left with:
x = tan^-1(3/y)
2x = tan^-1(y/4)
This means that the second one is two times the first (note the x), and we can combine them into one equation:
2tan^-1(3/y) = tan^-1(y/4)
If we plug this into our good friend Mathway.com, we find y to be approximately 5.745. That is the measure of segment AD. We now have the two legs of triangle ABD: 4 and 5.745. We find the hypotenuse by solving 4^2 + 5.745^2 = c^2. c is approximately 7.0004.
AB = 7.0004.
Simple Solution
ReplyDeleteIn Triangle ACD, < ACD = 90 - @
So in Triangle ABC, < BAC = 180 - 2@ - (90 - @) = 90 - @
So < BAC = < BCA
Hence BA = BC = 3 + 4 = 7
Sumith Peiris
Moratuwa
Sri Lanka
Solution 3
ReplyDeleteExtend CB to E such that AB = BE
Then < BAE = < BEA = @ = < CAD (since < ABC = 2@)
Hence Triangles ACD & AEC are similar (having angles @, < ACD)
and so < CAE = < ADC = 90
So B is the centre of Triangle ACE and AB = BC = 3+4 = 7
Sumith Peiris
Moratuwa
Sri Lanka