Geometry Problem 1495. Post your solution in the comment box below.
Level: Mathematics Education, K-12 School, Honors Geometry, College.
Details: Click on the figure below.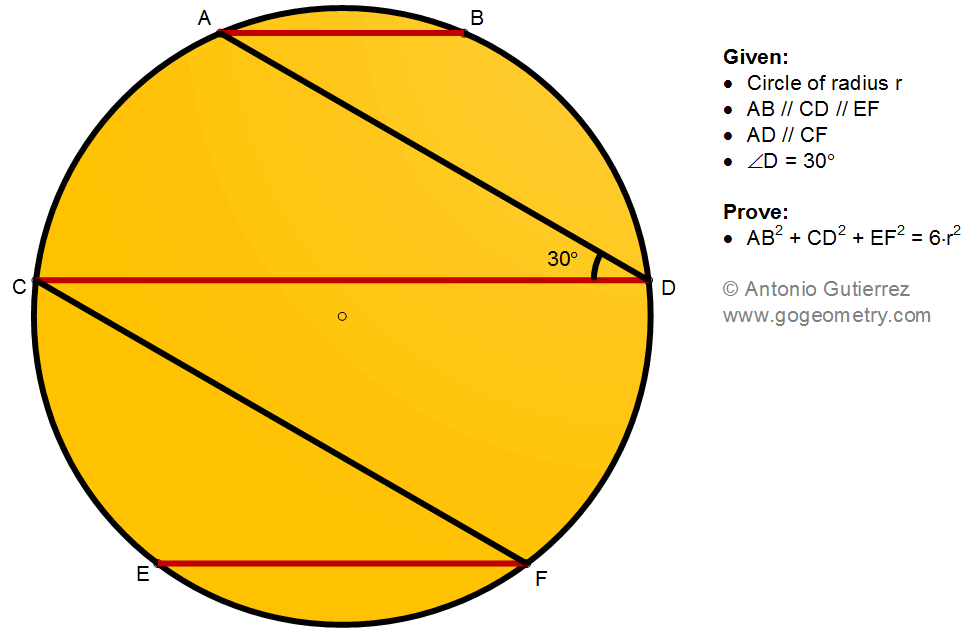
More Details
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
To post a solution to this problem click Comment underneath the post, or click into the line that says, “Enter Comment.” Type what you want to say and press Publish to post your solution.
Trigonometry Solution
ReplyDeleteIf O is the centre, Tr.s AOC, COE, DOF, BOD are all equilateral
So if < AOB = 2@ then < EOF = 120-2@
AB = 2r.sin@
CD = 2r.sin(60+@) = r.(sqrt3.cos@ + sin@)
EF = 2r.sin (60-@) = r.(sqrt3.cos@ - sin@)
Squaring and adding
AB^2 + CD^2 + EF^2
= r^2.( 4sin^2 @ + sin^2 @+ 3cos^2 @ + 2sqrt3.cos@sin@
+ sin^2 @ + 3cos^2 @ - 2sqrt3.cos@sin@)
= r^2.(6sin^2 @ + 6 cos^2 @)
= 6r^2
Sumith Peiris
Moratuwa
Sri Lanka
Geometry Solution using Pythagoras
DeleteLet AB = a, CD = b and EF = c. Let AH be the height of trapezoid ABCD, H on CD
Now AC = CE = BD = DF = r (they all subtend 60 degrees at the centre)
So CH = (b-a)/2, HD = (a+b)/2 and hence AH = (a+b)/(2sqrt.3)
Using Pythagoras for Tr. ACH, r^2 = (b-a)^2 /4 + (a+b)^2 /12,
from which 3r^2 = a^2 + b^2 - ab...........(1)
Similarly we can prove that
3r^2 = b^2 + c^2 - bc...............................(2)
(1) - (2) gives b = a + c ........(3) upon simplification assuming a not = to c
(1) + (2) gives 6r^2 = a^2 + b^2 + c^2 + (b^2 - ab - bc) and from (3)
the expression in the parenthesis = 0
Therefore a^2 + b^2 + c^2 = 6r^2
Sumith Peiris
Moratuwa
Sri Lanka
nice
ReplyDeleteI think this proof only goes in the special case when CD passes through O. Otherwise AD and DE are not equidistant and hence AC is not CE
ReplyDeleteI have not assumed that CD passes through O. Do read my proof carefully.
DeleteSumith Peiris
Geometry solution: It is not difficult to prove CD=EF+AB (1). Join B to F, from ABFE (Pt Theorem) we get CD²=3R² + AB . EF (2) From (1) and (2) we get the result
ReplyDelete