Geometry Problem. Post your solution in the comment box below.
Level: Mathematics Education, High School, Honors Geometry, College.
Click the diagram below to enlarge it.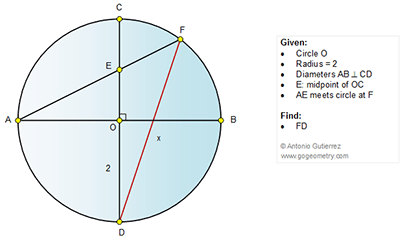
Saturday, February 28, 2015
Geometry Problem 1090. Circle, Diameters, Chord, Perpendicular, Metric Relations
Labels:
chord,
circle,
diameter,
metric relations,
perpendicular
Subscribe to:
Post Comments (Atom)
Let y= FB
ReplyDeleteWe have Triangle AOE similar to AFB => FA= 2.y
We have y^2+4y^2= 16 => y= 4/sqrt(5)
Applying Ptolemy's theorem in quad. ADBD we have
AB.FD=DB.AF+FB.AD
4.x= 2.sqrt(2).( 2y +y)
So x= 3.y.sqrt(2)/2
Replace value of y in above we have x= 12.sqrt(10)/5
Thanks Antonio
DeleteYes, The correct answer is 6.sqrt(10)/5.
the error is in the last step
Peter
cos∠FOD = -sin∠FOB
ReplyDelete= -2 sin∠FAB cos∠FAB
= -2×1/√5×2/√5
= -4/5
In ΔFOD,
x² = 2²+2²-2×2×2cos∠FOD = 72/5
x = 6√10 / 5
Observam ca AE=√5 (TP in trAOE) apoi CE.ED=FE.EA<=>1.3=√5.FE,teorema medianei in tr CFO ne da relatiaFE^2=[2(FO^2+FC^2)-CO^2]/4 si in final TP in tr CFD =>FO^2=CD^2-CF^2 =>x=4√21/5
ReplyDeleteObservam ca AE=√5 (TP in trAOE) apoi CE.ED=FE.EA<=>1.3=√5.FE,teorema medianei in tr CFO ne da relatiaFE^2=[2(FO^2+FC^2)-CO^2]/4 =>FE^2=8/5si in final TP in tr CFD =>FO^2=CD^2-CF^2 =>FO^2=16-8/5=>x=6√10 / 5
DeleteThanks Ion, the second is the right answer.
DeleteDraw FG perp to CD.
ReplyDeleteTriangles EFG, EAO are similar.
So FG/AO = GE/EO =EF/AE.
(i.e.) FG/2 = GE/1 = EF/√5.
Note AE.EF = DE.EC = 3*1 = 3.
(i.e.) √5*EF=3, EF = 3/√5.
So FG=6/5, GE=3/5, DG = 3 + 3/5 =18/5
So x^2 = DG^2 + FG^2
= 324/25 + 36/25 = 360/25.
Hence x = 6√10 / 5
Choose O as origin, lines AOB, COD as coordinate axes.
ReplyDeleteA=(-2,0),E=(0,1) imply equation of AE is x - 2y + 2=0.
Eq of the circle is x^2 + y^2 = 4
Solving these two equations, [x = 0, y = - 2] or [x = 6/5, y = 8/5]
So F=(6/5 ,8/5). Already D = (0,-2)
Hence DF^2 = 36/5 + 324/25 = 360/25, DF = 6√10 / 5
CF^2 = 16-x^2, AE • sqrt 5 and AD = sqrt 8
ReplyDeleteTr.s ECF and AED are similar so
(16-x^2)/8 • 1/5 from which x • 6/5sqrt10
Sumith Peiris
Moratuwa
Sri Lanka
Remark only: If G is the intersection of DF and AB, then S[DEG]=S[AEC].
ReplyDeleteHappy New Year everybody!
OE=1, OA=2, AE=sqrt5
ReplyDeletecos<OAE=2/sqrt5
<OEF=180-(90-<OAE)=90+<OAE
<AFD=45 & DE=3
Consider triangle DEF
sin<DEF/x=sin45/3
sin(90+<OAE)/x=sin45/3
cos<OAE/x=sin45/3
x=3cos<OAE/sin45
x=6sqrt10/5