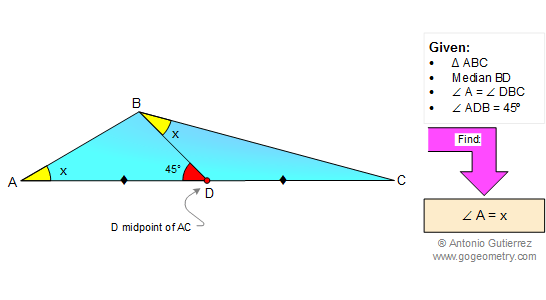
See complete Problem 1
Triangle, Angles, Midpoint, Congruence. Level: High School, SAT Prep, College geometry.
Post your solutions or ideas in the comments.
Sunday, May 18, 2008
Geometry Problem 1
Labels:
angle,
congruence,
midpoint,
triangle
Subscribe to:
Post Comments (Atom)
Problem 1
ReplyDeleteIn french, sorry...
On note H le pied de la hauteur issue de B.
On pose BH = h, AD = AC = 1.
En utilisant la trigonométrie dans les triangles ABH et BCH, rectangles en H, on obtient :
tan x = h/(1 - h)
et tan(45 -x) = h/(1 + h)
En utilisant tan(a - b) = ....
on arrive à l'équation :
2h² + 2h-1 = 0
qui a 2 solutions.
La solution positive est
(SQRT(3)-1)/2
Ce qui donne tan x = SQRT(3)/3
D'où x = 30°
ChrG.
consider similar triangle BDC and ABC,
ReplyDeleteDC/BC=BC/AC => DC/BC=1/√2=sin{x}/sin{45°} => x=30°
Could you please tell on how did you get DC/BC as 1/sqrt(2)
ReplyDeleteGood problem. Here is a solution:
ReplyDelete*Triangle BAC and ADC are similar in this order.
*AD is median of BC
*So by similarity and Appolonius' theorem we get AC=sq.rt2 times DC
and AB=sq.rt2 times AD
*AM be perpendicular on BC. (B-M-D-C)
*Triangle AMD is 45-45-90.
*So AD = sq.rt2 times AM.
*So AB = sq.rt2 times sq.rt2 times AM. i.e. AB = 2 times AM.
*Now AMB is right angle triangle,
where hypotenuse (AB) is two times one of the sides (AM). Hence is has to be 30-60-90 triangle.
*SO FINALLY ANGLE x = 30 degrees
on the fourth line of the solution it was possible to recall the sine theorem)
DeleteSmall correction
ReplyDeleteTriangles BDC and ABC are similar in that order.
In bad english. Sorry.
ReplyDeleteLet O the center of a circunference that contains points A,B and C. Extend segment BD to intersect circunference at point F. So ...
1. DO is perpendicular to AC. (D is midpoint)
2. Arc BC = Arc CF
3. CO is perpendicular to BF, intersecting at point E.
4. Triangle CED is retangle and isosceles.
5. Triangle OED is retangle and isosceles.
6. Triangle COD is retangle and isosceles.
7. OE = EC
8. Angle AOB = Angle EBC
9. sen x = OE/OB = 1/2
Then, x = 30 degrees.
Marcio, from Rio de Janeiro.
What is the justification for (3)? (CO is perpendicular to BF, intersecting at point E.)
DeleteMost likely because of the fact that the two arcs BC and CF are equal and adjacent. If you connect BF with a chord, this chord will be divided into two equal parts by the radius OC, which in this case will be perpendicular to that chord BF. (It wouldn't be the case if the arcs weren't equal.)
DeleteApply sine rule in Tr. BDC to get DC/BC=sinx/sin45 =V2sinx where V2=square root of 2. Likewise in Tr. ABC, BC/AC=V2sinx and 2DC = AC; hence 2V2sinxBC = BC/(V2sinx) or (sinx)^2 = 1/4.
ReplyDeleteTherefore, sinx=1/2 ignoring the negative sign since angles in a triangle can only be +ve and thus x=30 deg.
How may one prove this without using trigonometry?
Ajit: ajitathle@gmail.com
Dear Joe,
ReplyDeleteIt's possible to solve this problem without using trigonometry.
The key is auxiliary construction:
Geometry problem solving is one of the most challenging skills for students to learn. When a problem requires auxiliary construction, the difficulty of the problem increases drastically, perhaps because deciding which construction to make is an ill-structured problem. By “construction,” we mean adding geometric figures (points, lines, planes) to a problem figure that wasn’t mentioned as "given."
How about this for a plane geometry solution? From C drop a perpendicular to AB extended meeting it in N. Let CN = p. Angle NBC=45 from the given data. Hence angle BCN=45 and therefore BN=p and by Pythagoras, BC^2 = p^2+p^2=2p^2
ReplyDeleteNow triangles BDC & ABC are similar with angle BCD as the common angle & angle DBC=x=angle CAB. Hence AC/BC=BC/DC or BC^2=AC*DC=2DC^2 since D is the midpt. of AC. But as shown above BC^2=2p^2. So 2DC^2=2p^2 or DC =p. In other words, AC = 2p. Now in the rt. angled triangle ACN we've CN=p and AC=2p; hence ACN is 30-60-90 with angle NAC =30 deg. or x = 30 deg.
Ajit
ajitathle@gmail.com
nice solution!
DeleteLos triángulos ABC y BDC son semejantes por tener dos ángulos iguales. Sea AB=c, AC=b,BC=a Entonces c/BD=b/a=a/(b/2) De aqui se ve que b^2=2a^2 (b^2 es b al cuadrado) y BD=ac/b Al elevar al cuadrado esta igualdad y usando la otra igualdad se obtiene que BD^2 = (c^2)/2 Si se traza la altura BX se forma un triángulo rectángulo isósceles de catetos h Por Pitagoras se tiene que BD^2=2h^2 y comparando con la ultima igualdad se ve que c^2 = 4(h^2) y al sacar raíz cuadrada vemos que c = 2h En el triángulo rectángulo ABX la hipotenusa AB es el doble del cateto BX Luego, el ángulo opuesto a BX = h es 30º. Esto tiene demostracion no trigonometrica.
ReplyDeletesorry, my english is not god.i'm brazilian, but i think i have a better way to do it.i'll write it in portuguese:
ReplyDeleteprolongando o lado AB e formando um angulo de 90 com o lado AC.Assim teremos a mediana BD como mediana relativa a hipotenusa(sendo assim igual a mediana do triangulo ABC).ligando o angulo reto jah formado, perceberemos q este é isosceles, e formará outro isósceles EDC, logo, mexendo com os angulos(o q n é tão dificil) vc provará q este triangulo é equilatero mostrando q 2x= 60, logo = 30
http://ahmetelmas.files.wordpress.com/2010/05/cozumlu-ornekler.pdf
ReplyDeleteNote as in other solutions that triangle BDC is similar to triangle ABC, thus DC/BC=BC/AC. Let AD=DC=t, thus AC=2t.
ReplyDeleteCross-multiplying gives BC^2=2t^2, and BC=t*sqr(2).
Now drop an altitude from B in triangle ABD and from D in triangle BDC, and call them y and h, respectively. Since a median divides a triangle into two triangles with equal areas, yt=h(t*sqr(2)). solve for h=(sqr(2)/2)*y.
But the altitude from B creates a right, isosceles triangle, with hypotenuse BD, thus BD=sqr(2)*y. This means BD=2h, making a 30-60-90 triangle. QED using no trigonometry!
Here another approach: Assume x is not 30.
ReplyDeleteLet A', C' be such that <DA'B=30 and <DBC'=30.
(Triangle A'BC' is obtained by joining two equilateral triangles in opossite sides of a square.)
Now, it is easy to show that BD is also median of BA'C'.
Case 1: If A' is between A and D, by Euclid I.16, angle BAD is less than angle BA'D=30
but also angle DBC is greater than angle DBC'=30
As a consequence both angles can't be equal.
Which is a contradiction.
Case 2: If A is between A' and D the proof is analog.
Therefore A=A', C=C' and the result is clear.
:)
In order to assume that x is NOT 30°, one has to know first that it MIGHT BE 30°. This is putting the cart before the horse :q
DeleteLet O be the circumcentre of triangle ABC.
ReplyDeleteProduce BD to meet OC at E and the circumcircle at F.
Triangle FOC is isoceles with base angle 2x.
The semivertical angle of triangle is x.
X = 30
How do you presume point B lies on Circle O?
DeleteYou can construct a circle passing through ANY three points A, B, C. The trick is to choose its centre O wisely. But this can be done for any triangle: just erect a perpendicular bisector on each of its sides. All three perpendicular bisectors should coincide in one and only one point – the circumcentre of the triangle (i.e. the centre of the circle that passes through all three of its vertices A, B, C).
Deletesince BDC and BAC are similar
ReplyDeleteDC/BC=BC/AC
let DC=a
then BC=sqrt2 * a
Draw a half circle having it's Centre D and Diameter is AC
Extend AB to meet the half Circle at E
ABC=135 Deg
so, EBC=45 Deg
Since E=90Deg
ECB=45Dg
so BE=EC=a (As CB=sqrt2 * a)
Now Joint ED
ED=a (ED is another radius of half Circle)
so, EDC is eqlateral
So, EDC=60 Deg
as EDC=2*EAC
EAC=30 Deg
The easiest and most succint solution:
ReplyDeleteTriangle ABC & triangle BDC are similar.
Therefore, BC/CD=AC/BC=AB/BD.
Taking BC/CD=AC/BC, we get, BC.BC=2CD. CD
So, BC=sqrt (2). CD
Taking BC/CD=AB/BD, we get, AB=sqrt (2). BD
Let, AB= c
So, BD=c/sqrt (2)
Dropping an altitude BE in triangle ABD, we get a right isosceles triangle whole hypotenuse is BD and BD=c/sqrt (2)
So the legs: BE=ED=c/2
Now we see that the triange ABE is a right triange with sides AB=c, BE=c/2 and AE=c. sqrt (3)/2
This clearly implies
ABE to be a 30-60-90 triangle.
Therefore, Angle BAE= x= 30 degree.
Two solutions, the first bye me, and the second by my friend.
ReplyDeletehttp://www.youtube.com/watch?v=MEv_-R0mIKc
Greetings.
1st problem solution
ReplyDeleteapply sine rule to triangle ABD
AD/sin(135-x)=BD/sin(x) then
BD=ADxSIN(X)/SIN(135-X) PUTTING IT ASIDE
APPLY SINE RULE TO TRIANGLE BDC
DC/SIN(X)=BD/SIN(45-X)
BD=ADxSIN(45-X)/SIN(X) EQUATING 1&2 WE GET
ADxSIN(X)/SIN(135-X)=DCxSIN(45-X)/SINX
SIN2(X)=2SIN(45-X)xCOS(45-X)/2
SIN2(X)=SIN(90-2X)/2=COS(2X)/2
SIN2(X)=1-SIN2(X)/2
4SIN2(X)=1
SIN(X)=1/2
:X=30
Video solution (Spanish version) by Eder Contreras and Cristian Baeza at Geometry problem 1.
ReplyDeleteSolution sent by Petre CIOBANU
ReplyDeleteHello
another solution of #1 here
unfortunately is now written in Romanian (a language of Latin origin).
I respected the request to use the basic methods.
I write here because I could not post the message box with solutions.
I would be glad that you appreciate my solution.
Thanks and congratulations for the site,
Petre CIOBANU
corect link http://ogeometrie-cip.blogspot.ro/2012/08/problema-1.html
Deleteangle BDC = 180 - angle BDA
ReplyDelete= 180 - 45 = 135 degree
we also know that angle BDC = angle DAB + angle ABD
= x + angle ABD
ie angle ABD = (135-x)degree
now AD/sin(angle ABD)= BD/sin x
or BD/AD = sin x/ sin(135-x)........... 1
for triangle BDC
DC/sin(angle DBC)=BD/sin (angle BCD)
BD/DC= sin (angle BCD)/sin(angle DBC) = sin(45-x)/sin x...............2
from 1 and 2 we get
BD/AD=BD/DC [as AD=DC]
sin x/ sin(135-x)=sin(45-x)/sin x
or (sin x)^2 = sin(135-x)sin(45-x)
or (sin x)^2 = 1/root2(cos x + sin x) . 1/root2 (cos x - sin x)
or (sin x)^2 = 1/2[ (cos x)^2- (sin x)^2]
or 2.(sin x)^2=[ (cos x)^2- (sin x)^2]
or 3.(sin x)^2=(cos x)^2
or (tan x)^2 = 1/3
or tan x =1/root3
or x=30 degree
Let AD = DC = t.
ReplyDeleteAs seen above, [BDC] and [ABC] are similar => BC = sqrt(2) t.
Drop a perpendicular from C to AB produced cutting it at E and let BE = s.
By considering angle(EBD) as an exterior angle to [ABD], we have angle(EBC) = 45 degrees.
EBC is then an 45–45–90 triangle with EC = s and BC = sqrt(2) s
Thus, s = t
In [AEC],
EC = t, AC = 2t and angle(E) = 90 degrees => AEC is an 30–60–90 triangle.
Therefore, x = 30 degrees
Mike from Canotta
Let AD=DC=a
ReplyDeleteSince BDC and ABC are similar BC=V2a
now arBAD = arBDC or 1/2. a. BD. sin 45 = 1/2. BD. V2 a. sin x
sin x = 1/2 since x is acute so x = 30 degrees
This is a very good problem
ReplyDeletehere is the solution hope you understand it
Stratergy:In this problem we need to show that Tri BAEis 30-60-90(BE IS THE ALTITDE)for this we will use the thereom if one side of an right angeled Tri is half the hypotenuse the opp Ang is =30
PROOF
TriBDC and TriABC are similar
BC/AC=DC/BC=BD/AB-----1
considerDC/BC=BC/AC
let DC=a
then BC=sq
CONSTRUCT Tri BED(BE IS THE ALTITDE)
LET BD=y
Th EB=ED=y/sqrt2---2
Using 1
BA/BD=BC/DC
sqrt2*y/y=AB/y
Th sqrt2*y=AB-----3
Using the Stratergy
if BE*2=AB
THE PROOF IS COMPLETE
USING 1,2,3TO FILL VALUES WE GET
Y/sqrt2*2=BE
sqrt2*sqrt2*x/sqrt2=BE(2=sqrt2*sqrt2)
simplifying we get
BE=sqrt2*x
AB=sqrt2*x
AB=BE
Using Stratergy
x=30
Hence proveD
Take P - symmetrical of C about AB; clearly tr. BCP is right-angled and isosceles, hence <BPC=45=<ADB and BDCP is cyclic, so PD_|_AC, i.e. PC=AP, but by symmetry AP=AC and ACP is an equilateral triangle, or <BAC=30 degs. Best regards, Stan Fulger
ReplyDeleteSince Tr.s ABD & BDC are equal in area, BD/sqrt2 X AD = DE X BC where DE is the altitude. But since BC is tangential to Tr. ABD, BC = sqrt 2 X AD from which we deduce that DE = 1/2 BD and so x = 30
ReplyDeleteSumith Peiris
Moratuwa
Sri Lanka
The symmetrical of AC about AB and BC respectively intersect at E; since <BAC+<BCA=45, we infer <AEC=90 and B is the incenter of triangle AEC, hence <AEB=45=<ADB, consequently triangles AEB and ADB are congruent (a.s.a criterion), making AE=AD. From right-angled triangle AEC we get DE=AD, triangle ADE equilateral and <EAD=60, consequently <BAD=30
ReplyDeletehttps://www.facebook.com/photo.php?fbid=10206189617728061&set=a.10205987640598759.1073741831.1492805539&type=3&theater
ReplyDeleteThe circumscribed circl with triangle BCD intersects the perpendicular bisector AC in E. Then AE=EC and <DAB=<DBC=<DEC=x. If AB intersects EC in K so <DAK=<DEK=x .Is BK perpendicular EC(<KBC=<KAC+<BCD=<DBC+<BCD=45=<KBE ),then BC=BE, EK=KC. But triagle AKC=triangleAKE,so AE=AC <BAC=x=<BAE and triangle AEC it is equilateral. Therefore 2x=60
ReplyDeleteOr x=30.
Do you mean circumscribed circle of ABC
Deleteor BCD?
https://www.youtube.com/watch?v=I1wHTSSUW-w
ReplyDeleteLet E, be a point on (AD) ̅ such that (BE) ̅⊥(BD) ̅.
ReplyDeleteLet F, be a point on (AD) ̅ such that (BF) ̅⊥(AD) ̅.
m∠EBD=m∠BFD=m∠BFE=90°
∆EBD,∆BFD and ∆BFE are isosceles right triangles.
BF=EF=FD=a, FA=b
AD=CD
AD=DC=AF+FD=a+b, AE=AF-EF=b-a
BD=BE=√2 a
m∠BEF=m∠EBF=m∠FBD=45°
m∠AEB=m∠BDC=135°
∆AEB~∆BDC
(√2 a)/(a+b)=(b-a)/(√2 a), 2a^2=b^2-a^2,3a^2=b^2, then b=√3 a
c^2=a^2+b^2=a^2+(√3 a)^2=4a^2, c=2a
∆ABF is a 30°-60°-90° triangle with m∠A=x=30°
see video : Problem 1 Solution A
ReplyDeleteTake a pen and a pice of paper, and illustrate accordingly.
ReplyDeleteLabel angle BCD as y. Now, x + y = 45.
Label angle ABD as z. Now, x + z = 135.
Firstly, add a point E and connect it to point A with line AE, and to point B with line BE, such that a duplicate of triangle ABD is formed. Since triangles ABE and ABD are identical, we can conclude that AD = AE, BD = BE.
Next, add a point F and connect it to point A with line FA, and to point B with line FB, such that a duplicate of triangle BCD is formed. Since triangles BCD and BCF are identical, we can conclude that CF = CD, BF = BD.
Now, we connect point E to point F with line EF. This is where the magic happens!
Angle EBF will be:
360 - x - y - x - y = 360 - 135 - 135 = 90
BD = BE
BD = BF
Therefore, triangle EBF is an isosceles right angled triangle. This means that angle BEF = angle BFE = 45.
Angle BFE + angle BFC = angle BFE + angle BDC = 45 + 135 = 180. This shows that E, F and C are collinear. Angle AEC = angle AEB + angle BEC = angle ADB + angle BEF = 45 + 45 = 90.
Line AE = line AD. Line AC = 2 of line AD. Angle AEC = 90. These are properties of a 30-60-90 triangle.
Therefore, 2x = 60, and x = 30.
Tr. ABC Similar to BDC
ReplyDelete=>BC/AC=DC/BC
=>BC^2=CA.CD ------(1)
Also given m(DBC)=m(BAD) -----(2)
From (1)&(2), CB is tangent to circumcircle of ABD. Let O be the center of this circle.
let AD=DC=a=> BC=a.Sqrt(2)
From the same similarity
AB/BC=BD/DC=>AB=BD.Sqrt(2)--------(3)
Since m(BDA)=45=>m(BOA)=90=>AOB is 45-90-45 triangle=>AB=BO.Sqrt(2)----(4)
From(3)&(4) OB=BD=Radius of the circumcircle.
However OB=OD=> BOD is an equilateral triangle
m(OBD)=90-x=60=>x=30 or m(BOD)=2.m(BAD)=2x=60=>x=30 degrees
Solution 2
ReplyDeleteDrop a perpendicular CE from C to AB extended
Easily Tr.BCE is right isosceles and so CE = a/sqrt2 .....(1)
Since CB is tangential to Tr. ABD at B, a = b/sqrt2 ....(2)
From (1) and (2) CE = b/2 and hence ACE is a 30-60-90 Triangle
Therefore x = 30
Sumith Peiris
Moratuwa
Sri Lanka
See the drawing
ReplyDeleteLet b=AD=DC and d=BC
ΔACB and ΔBCD are similar since ∠BAC=∠DBC=x and ∠BCD=∠BCA
Then AC/BC=CB/CD=AB/BD => 2b/d=d/b => d=b√2
Define C’ such as DC’ ⊥ AC and DC’=b
∠BDC=∠ADC - π/4= π - π/4 = 3 π/4
∠BDC’=∠BDA + ∠ADC’ = π/4 + π/2 = 3 π/4
=> ∠BDC= ∠BDC’
=>Δ BDC is congruent to ΔBDC’
=>BC=BC’=d and ∠DBC’=∠DBC=x => ∠C’BC=2x
DC’ ⊥ DC and DC’=DC=b => CC’ = b√2=d
ΔBCC’ is equilateral
∠C’BC = 60°=2x
Therefore x=30°
Problem 1 Solution:
ReplyDelete1. triangles ACB and BCD are similar: x = x, and <C = <C AA~ Theorem.
2. let AD = DC = a, let BC = b: a/b = b/(2a) so b/a = 1/sqrt2
3. Since the two triangles are similar, and m<BDC = 135 (linear pair with <ADB = 45), then m<ABC = 135.
3. Extend AB. Drop an altitude from C to line AB. Call the intersection E. m<EBC = 45.
4. Since m<AEC = 45 (altitude) and m<EBC = 45, triangle ECB is right isosceles: BE = EC. and BC is sqrt 2 times BE or EC.
5. Since, step 2, BC is sqrt 2 times DC, DC = BE = EC. Equilateral. m<ECD = m<CDE = m<DEC = 60.
6. Angle addition, 60 - 45 = 15 = m<BCD.
7. Triangle angle sum : 180 = 135 + 15 + x... x = 30.