Thursday, December 4, 2025

Geometry Problem 1610: Area of a Curvilinear Triangle in a Rhombus

Challenging Geometry Problem 1610. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.

Gain comprehensive insights! Click below to reveal the complete details.

Illustration of Geometry Problem 1610
Click for additional details.

Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.



at

4 comments:

  1. AnonymousDecember 5, 2025 at 5:40 PM

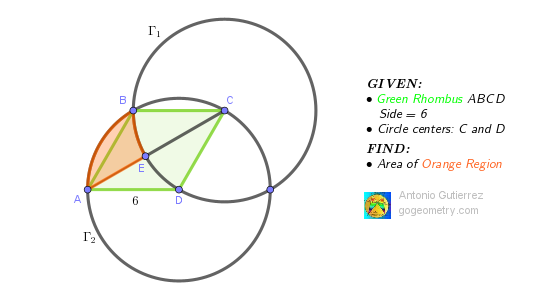
    Since the area of the orange region equals the area of sector BCD, 36π × (30°/360°) = 12π.

    Simply construct sector BAD centered at A and line segment BD.

    ReplyDelete
  2. AnonymousDecember 5, 2025 at 5:43 PM

    Correction

    Since the area of the orange region equals the area of sector BCD, 36π × (30°/360°) = 3π.

    Simply construct sector BAD centered at A and line segment BD.

    ReplyDelete
  3. SUMITHLC63December 7, 2025 at 2:54 AM

    The Rhombus obviously has angles 120,60,120,60

    In Circle T2, Area within Arc ABC = Pi.6^2 /3 - V3. 6^2 / 4 = 12Pi - 9V3
    I(In Circle T1, Area of Circular Section CEB = Pi.6^2 / 12 = 3Pi

    Subtracting, Orange Area = 9(Pi - V3)

    Sumith Peiris
    Moratuwa
    Sri Lanka

    ReplyDelete
    Replies
    1. AnonymousDecember 7, 2025 at 2:49 PM

      The area of the bow-shaped figure with BC as the chord must also be reduced.

      Delete

Share your solution or comment below! Your input is valuable and may be shared with the community.