Challenging Geometry Problem 1608. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.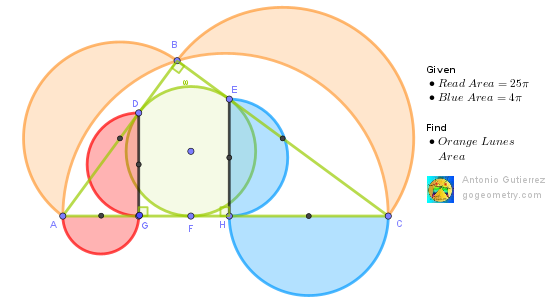
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
With the usual notation, AD = s - a & CE = s - c
ReplyDeleteLet DG = 2p, AG = 2u, EH = 2q & HC = 2v
Now Red Area = 25 Pi = Pi (p^2 + u^2)/2 = Pi(s - a)^2 / 8
So s - a = 10 V2 ..... (1)
Blue Area = 4Pi = Pi (q^2 + v^2)/2 = Pi(s - c)^2 / 8
So s - c = 4 V2 ...... (2)
(1) X (2) ; (s - a)(s - c) = 80
(b + c - a)(b + a - c)/4 = 80
b^2 - (a - c)^ 2 = 320
But b^2 = a^ + c^2
So ac / 2 = 80 ....(3)
Now Orange Area = Pi(c^/4 + b^2/4) /2 - (Pi b^2 /4) / 2 + ac / 2 = ac /2
(since b^2 = c^2 + a^2)
So Orange Area = 80 (from (3))
Sumith Peiris
Moratuwa
Sri Lanka
First, note that in a right triangle, the sum of the areas of the two semicircles whose diameters are the two sides adjacent to the right angle is equal to the area of the semicircle whose diameter is the hypotenuse.
ReplyDeleteFrom Red Area = 25π,
solving π*(AD/2)^2*(1/2) = 25π gives AD = 10√2.
Similarly, we obtain EC = 4√2.
Let BD = BE = a. Since ⊿ABC is a right triangle,
(a + 10√2)^2 + (a + 4√2)^2 = (14√2)^2
Solving this gives a = -7√2 + √178.
Using the initial observation, we see that the Orange Lunar Area = △ABC Area.
Therefore,
Orange Lunes Area = (1/2) * (a + 10√2) * (a + 4√2) = 80