Challenging Geometry Problem 1607. Share your solution by posting it in the comment box provided.
Audience: Mathematics Education - K-12 Schools, Honors Geometry, and College Level.
Gain comprehensive insights! Click below to reveal the complete details.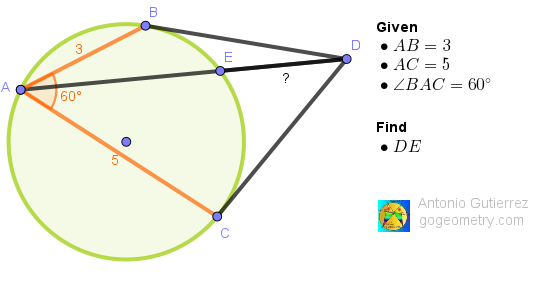
Click for additional details.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Share your solution by clicking 'Comment' below the post or entering your solution or comment in the 'Enter Comment' field and pressing 'Publish'.
Let BE =a, CE = b, AE = c, DE = d and BD = CD = t
ReplyDelete<CBD = <BCD = 60 hence Triangle BCD is equilateral and
BC^2 = t^2 = 3^2 + 5^2 - 2.3.5.cos60 = 19.............(1)
Now Triangle BED // Triangle ABD hence
a = 3d/V19 ..............(2)
Similarly b = 5d/V19 ........(3) since Triangles CED // ACD
Using Ptolemy in cyclic quadrilateral ABEC,
5a + 3b = V19.c and substituting from (1) and (2) and simplifying
30d/V19 = V19. c from which,
c = 30d/19
Now d (c+d) = 19 so
d (30d/19 + d) = 19 hence
d^2 = 19^2/49 and therefore
d = 19/7 = DE
Sumith Peiris
Moratuwa
Sri Lanka
Alternate Solution using the same letters as before. Let < BAD = @
DeleteConstruct Equilateral Triangle AFD, F and C on the same side of AD
Triangles FCD and ABD are congruent SAS and so
< DFC = < DAB = @ = < DBE so < EBC = < EAC = 60 - @ and so < CAF = @
Since DFC = @, < CFA = 60 - @ and so < ACF = 120
Hence AF^2 = 5^2 + 3^2 - 2.3.5.cos 120 and so
AF = 7 = AD = c + d
Hence DE d = d = BD^2 / (c + d) = 19 /7
Sumith Peiris
Moratuwa
Sri Lanka
Let ∠ABC=θ.
ReplyDelete△Using the cosine law on ABC:
cosθ=1/(2√19), sinθ=5√3/(2√19)
△Using the cosine law on ABD:
AD^2=3^2+(√19)^2-1*3*√19*cos(60°+θ)=49
Therefore, AD=7
Since DE*DA=19, DE=19/7
Rotate △ABD 60° about point D.
ReplyDelete(Point B coincides with point C, and point A moves to the new point A')
Then, △AA'D becomes an equilateral triangle.
Let ∠CAD = θ. Then, ∠AA'C = θ.
Applying the cosine rule to △ACD and △AA'C:
cosθ = (25 + AD² - 19) / (2 × 5 × AD) = (9 + AD² - 25) / (2 × 3 × AD)
Solving this gives
AD = 7.