Geometry Problem
Level: Mathematics Education, High School, Honors Geometry, College.
Click the figure below to see the complete problem 858.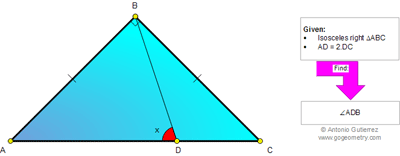
Thursday, February 14, 2013
Problem 858: Isosceles Right Triangle, Cevian, Ratio 2:1, 45 Degrees, Congruence, Angles, Auxiliary Lines
Subscribe to:
Post Comments (Atom)
Reflect B along AC to E to form a square ABCE.
ReplyDeleteLet BD cut CE at F.
Tr.(ABD) ~ Tr.(DCF) with length ratio 2:1.
CF = (1/2)AB = (1/2)BC.
Therefore, BCF is a 30-60-90 triangle.
Angle DBC = Angle FBC = 30.
x = 45 + 30 = 75
To W Fung, please review. Triangle BCF is not a 30-60-90 triangle.
DeleteSorry, my mistake.
Deleteit should be using problem 848, angleFBC is ~26.5
x = 45 + 26.5 = 71.5
E midpoint of the DA
ReplyDeleteEF perpendicular to BC .
Then,CFE ,is .rectangular and isosceles triangle.So, AE=ED=DF and FD ,isperpendicular to AC .
from problem 848 , angle FAE= 26,5 .But,FDAB is,cyclic quadrilateral.Therefore ,angle DBC=26,5
So,x=26,5+45=71,5 degrees
plan: http://img703.imageshack.us/img703/3806/geogebra2.png
If AB=1 and AC = sqrt2, than AD (2/3)sqrt2. Law of cosines a^2 = b^2 + d^2 - 2bdcos(A)(where a= BD, b=AD and d=AB). Use this value in law of sines sinD/d = sinA/a. Angle ABD = 71.565
ReplyDeleteTrazar la altura BH, considere AD=4 y DC=2 (sin perdida de generalidad), entonces HD=1 pues BH es altura y mediana por ser el triangulo ABC rectangulo e isósceles, luego BH=HC=3, pues el triangulo rectangulo BHC es 45° - 45°, asi el triangulo rectangulo BHD tiene por catetos 1 y 3 es decir es notable, finalmente x=143°/2=71,5°
ReplyDeleteBy Tino