Geometry Problem
Level: Mathematics Education, High School, Honors Geometry, College.
Click the figure below to see the complete problem 857.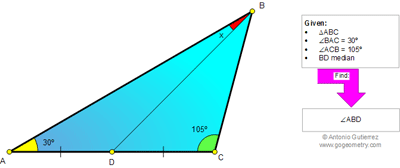
Tuesday, February 12, 2013
Problem 857: Triangle, Median, Midpoint, Angles, 30, 45 Degrees, Congruence, Auxiliary Lines
Labels:
30 degrees,
45 degrees,
angle,
auxiliary line,
congruence,
median,
triangle
Subscribe to:
Post Comments (Atom)
CA ,perpendicular to AB. Then, angle ACE=60 ,and angle ECB=45.
ReplyDeleteBecause, angle EBC=45 ,EC=EB=ED=DA. So , 2x=30 ,x=15 degrees
http://img571.imageshack.us/img571/3688/p857trianglemedianmidpo.gif
Reflect C along AB to a point E.
ReplyDeleteAngle(EBC)=2*Angle(ABC)=2*(45)=90
By reflection, Triangle(AEC) is equiliteral and
since AD=DC, Angle(EDC)=90.
So, E,D,B,C are concyclic.
x = Angle(ABC)-Angle(DBC)
= 45 - Angle(DEC)
= 45 - (1/2)*(Angle(AEC))
= 45-30
= 15.
http://img42.imageshack.us/img42/6031/problem857.png
ReplyDeleteDraw CE ⊥AB
We have ∠ (ACE)= 60 and ED is a median of right triangle AEC
So ED=DA=DC
We have ∠ (ECB)=105-60=45 => EC=EB=ED
∠ (AED)=30=2.x =>x=15
This kind of problems usually are solvable by placing the circumcenter.
ReplyDelete- Let O be the circumcenter of (ABC).
- AD=OD=CD, so tr DOB is isosceles.
- tr OBC is equilateral.
- ODCB is a deltoid, so BD is perp to OC and <OBD=30°.
- <OBA=<OAB=15°.
Finally <x=15°.
http://www.mathematica.gr/forum/viewtopic.php?f=20&t=35316&p=162751
ReplyDelete